| Codeforces Round 737 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача.
ICPC Assiut Community решили провести уникальное соревнование по шахматам, и вы были выбраны для того, чтобы контролировать ферзя и выслеживать прячущегося короля. Его, в свою очередь, будут контролировать члены ICPC Assiut Community.
Вы играете на шахматной доске $$$8\times8$$$, строки которой нумеруются сверху вниз, а столбцы — слева направо. Клетка в строке $$$x$$$ и столбце $$$y$$$ обозначается как $$$(x, y)$$$.
За один ход вы можете переместить ферзя на любую клетку на той же горизонтали, вертикали или любой из двух диагоналей. Например, если ферзь был в клетке ($$$4$$$, $$$5$$$), вы можете переместиться на ($$$q_1$$$, $$$5$$$), ($$$4$$$, $$$q_1$$$), ($$$q_1$$$, $$$9-q_1$$$) или ($$$q_2$$$, $$$q_2+1$$$), где ($$$1 \le q_1 \le 8$$$, $$$q_1 \ne 4$$$, $$$1 \le q_2 \le 7$$$, $$$q_2 \ne 4$$$). Заметьте, что ферзь не может оставаться на месте.
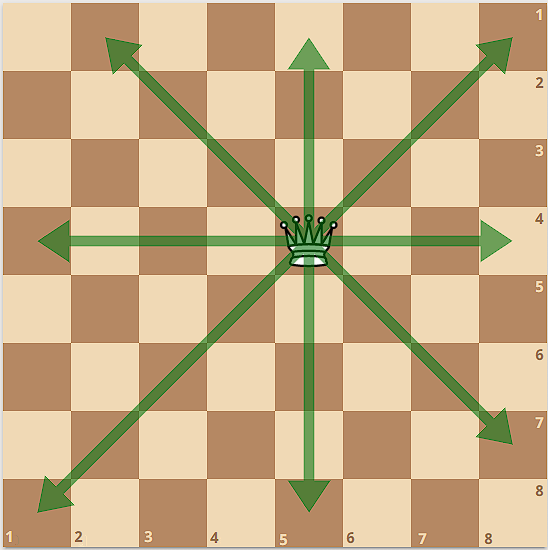
За один ход король может переместиться «Вправо», «Влево», «Вверх», «Вниз», «Вниз-Вправо», «Вниз-Влево», «Вверх-Влево», или «Вверх-Вправо» так, чтобы оставаться на доске. Король не может ходить в клетку, находящуюся на одной горизонтали, вертикали или диагонали с ферзем (включая клетку, где стоит ферзь). Например, если король был на клетке ($$$4$$$, $$$5$$$), он может сходить в ($$$4+k_1$$$, $$$5+k_2$$$) где ($$$-1 \le k_1,k_2 \le 1$$$, $$$(k_1, k_2) \ne (0, 0)$$$).
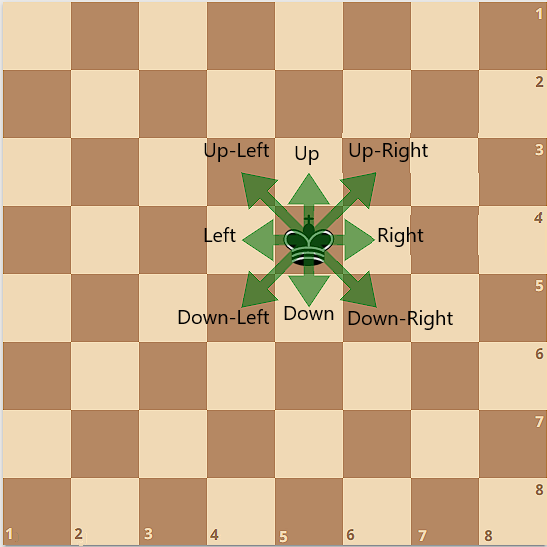
В начале игры вы должны разместить ферзя на любую клетку на доске. После этого король тайно размещается на одной из свободных клеток. Вы не знаете позиции короля. Затем, король и ферзь по очереди делают ходы. Король ходит первый. Ходы короля проходят в одном из возможных направлений («Вправо», «Вниз», «Вверх-Влево», и т.д.). Вам будет известно только направление хода. После этого вы должны совершить ход ферзем. Для этого сообщите клетку, на которую вы хотите сходить. Игра продолжается до тех пор, пока вы не выиграете или у вас не закончатся ходы.
Вы выигрываете, если у короля нет доступных ходов. Вы проигрываете после $$$130$$$ ходов ферзя, если король имеет доступный ход.
В первой строке содержится целое число $$$t$$$ ($$$1 \le t \le 60$$$) — количество наборов входных данных.
В каждом наборе входных данных сначала выведите стартовую позицию ферзя. Если вы поставите его в клетку с королем - вы сразу победите.
После этого вы можете сделать не более $$$130$$$ ходов. Каждый ход делается в формате $$$x$$$ $$$y$$$, где $$$x$$$ и $$$y$$$ — это два целых числа ($$$1 \leq x,y \leq 8$$$), обозначающих строку и столбец новой позиции ферзя. Ваши ходы должны быть корректными ходами ферзя.
После изначального размещения ферзя и после каждого вашего хода считайте строку $$$s$$$, которая обозначает направление хода короля. Это будет одна из следующих строк: «Right», «Left», «Up», «Down», «Down-Right», «Down-Left», «Up-Left», «Up-Right», или «Done», если вы победили в игре. Вы должны расценивать «Done» как конец очередного набора входных данных.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если в любой момент времени вы совершите недопустимый ход или сделаете более $$$130$$$ ходов, игра завершится моментально и вы получите вердикт Неправильный ответ.
1 Left Right Done
7 5 7 6 7 7
В примере король находится в клетке $$$(8, 8)$$$ в начале. Игра проходит следующим образом:


| Название |
|---|




