| Codeforces Round 735 (Div. 2) |
|---|
| Закончено |
Вам дано дерево с $$$n$$$ вершинами. Напомним, что дерево — это связный неориентированный граф без циклов.
Пусть $$$a_1, a_2, \ldots, a_n$$$ — последовательность целых чисел. Выполним следующую операцию ровно $$$n$$$ раз:
- Выберем неудаленную вершину $$$u$$$. Присвоим $$$a_u :=$$$ количество неудаленных вершин, соседних с $$$u$$$. Затем удалим вершину $$$u$$$ вместе со всеми ребрами, концом которых она является.
Для каждого целого числа $$$k$$$ от $$$1$$$ до $$$n$$$ найдите по модулю $$$998\,244\,353$$$ количество различных последовательностей $$$a_1, a_2, \ldots, a_n$$$, удовлетворяющих следующим условиям:
- можно получить $$$a$$$, выполнив вышеупомянутую операцию ровно $$$n$$$ раз в некотором порядке.
- $$$\operatorname{gcd}(a_1, a_2, \ldots, a_n) = k$$$. Здесь $$$\operatorname{gcd}$$$ означает наибольший общий делитель элементов в $$$a$$$.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10\,000$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$).
Каждая из следующих $$$n - 1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$), указывающих на наличие ребра между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что заданные ребра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$3 \cdot 10^5$$$.
Для каждого набора входных данных выведите в одной строке $$$n$$$ целых чисел, где для каждого $$$k$$$ от $$$1$$$ до $$$n$$$ $$$k$$$-е целое число обозначает ответ, когда $$$\operatorname{gcd}$$$ равен $$$k$$$.
2 3 2 1 1 3 2 1 2
3 1 0 2 0
В первом наборе входных данных дерево изображено на рисунке.
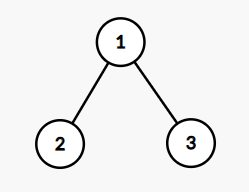
- Если мы удалим вершины в порядке $$$1 \rightarrow 2 \rightarrow 3$$$ или $$$1 \rightarrow 3 \rightarrow 2$$$, то полученная последовательность будет $$$a = [2, 0, 0]$$$, которая имеет $$$\operatorname{gcd}$$$, равный $$$2$$$.
- Если удалить узлы в порядке $$$2 \rightarrow 1 \rightarrow 3$$$, то полученная последовательность будет $$$a = [1, 1, 0]$$$, $$$\operatorname{gcd}$$$ которой равен $$$1$$$.
- Если удалить узлы в порядке $$$3 \rightarrow 1 \rightarrow 2$$$, то полученная последовательность будет $$$a = [1, 0, 1]$$$, $$$\operatorname{gcd}$$$ которой равен $$$1$$$.
- Если удалить узлы в порядке $$$2 \rightarrow 3 \rightarrow 1$$$ или $$$3 \rightarrow 2 \rightarrow 1$$$, то полученная последовательность будет $$$a = [0, 1, 1]$$$, $$$\operatorname{gcd}$$$ которой равен $$$1$$$.
Обратите внимание, что здесь мы считаем количество различных последовательностей, а не количество различных порядков удаления узлов.
| Название |
|---|




