Рассмотрим последовательность различных целых чисел $$$a_1, \ldots, a_n$$$, каждое из которых соответствует отдельной вершине графа. Будем соединять две вершины ребром, если соответствующие им числа не взаимно просты, т. е. если они имеют общий делитель, больший чем $$$1$$$.
Вам даны $$$q$$$ запросов, в каждом запросе вы хотите попасть из вершины, соответствующей значению $$$a_s$$$, в вершину, соответствующую $$$a_t$$$. Для того чтобы это сделать, вы можете выбирать существующее значение $$$a_i$$$, создать новую вершину со значением $$$a_{n+1} = a_i \cdot (1 + a_i)$$$ и соединить ее со всеми вершинами, значения которых не взаимно просты с $$$a_{n+1}$$$. После этого $$$n$$$ увеличивается на $$$1$$$. Вы можете повторять эту операцию любое количество раз, удлиняя последовательность, и, возможно, получая одинаковые значения. Какое минимальное количество вершин нужно добавить, чтобы $$$a_t$$$ стало достижимо из $$$a_s$$$?
Обратите внимание, что запросы независимы. В каждом запросе вы начинаете с исходной последовательности $$$a$$$, заданной во входных данных.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$2 \leq n \leq 150\,000$$$, $$$1 \leq q \leq 300\,000$$$) — размер исходной последовательности и количество запросов.
Вторая строка содержит $$$n$$$ различных целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$2 \leq a_i \leq 10^6$$$, $$$a_i \neq a_j$$$, если $$$i \ne j$$$).
$$$j$$$-я из следующих $$$q$$$ строк содержит два различных целых числа $$$s_j$$$ и $$$t_j$$$ ($$$1 \leq s_j, t_j \leq n$$$, $$$s_j \neq t_j$$$) — индексы вершин для $$$j$$$-го запроса.
Выведите $$$q$$$ строк. $$$j$$$-я строка должна содержать одно целое число: минимальное количество вершин, которое нужно добавить, чтобы можно было достичь $$$a_{s_j}$$$ из $$$a_{t_j}$$$.
3 3 2 10 3 1 2 1 3 2 3
0 1 1
5 12 3 8 7 6 25 1 2 1 3 1 4 1 5 2 1 2 3 2 4 2 5 3 1 3 2 3 4 3 5
0 1 0 1 0 1 0 1 1 1 1 2
В первом примере вы можете добавить вершину со значением $$$2 \cdot 3 = 6$$$, или $$$10 \cdot 11 = 110$$$, или $$$3 \cdot 4 = 12$$$. Ни одно из этих добавлений не нужно в первом запросе, так как вы уже можете добраться из $$$a_1 = 2$$$ в $$$a_2 = 10$$$.
Во втором запросе оптимальным является добавление вершины со значением $$$6$$$ или $$$12$$$. Например, добавляя вершину со значением $$$6$$$, мы сможем добраться из $$$a_1 = 2$$$ в $$$a_3 = 3$$$ по пути со значениями $$$(2, 6, 3)$$$.
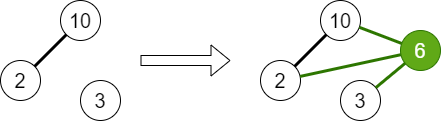
В последнем запросе второго примера мы хотим добраться из $$$a_3 = 7$$$ в $$$a_5 = 25$$$. Одним из возможных способов достичь это является создание вершины со значением $$$6 \cdot 7 = 42$$$, а затем создание вершины со значением $$$25 \cdot 26 = 650$$$. В финальном графе, состоящем из 7 вершин, существует путь из $$$a_3 = 7$$$ в $$$a_5 = 25$$$.
| Название |
|---|




