| Codeforces Global Round 15 |
|---|
| Закончено |
На окружности лежат $$$2n$$$ различных точек, обладающих следующим свойством: как бы вы ни выбрали $$$3$$$ хорды, соединяющие $$$3$$$ непересекающиеся пары точек, ни одна точка строго внутри окружности не принадлежит всем $$$3$$$ хордам. Точки нумеруются $$$1, \, 2, \, \dots, \, 2n$$$ по часовой стрелке.
Изначально $$$k$$$ хорд соединяют $$$k$$$ пар точек таким образом, что все $$$2k$$$ концов этих хорд различны.
Необходимо провести еще $$$n - k$$$ хорд, которые соединят оставшиеся $$$2(n - k)$$$ точек (каждая точка должна быть концом ровно одной хорды).
Пусть $$$x$$$ — это общее количество пересечений всех $$$n$$$ хорд. Вычислите максимальное значение, которого может достичь $$$x$$$ при оптимальном выборе $$$n - k$$$ хорд.
Обратите внимание, что точное расположение точек $$$2n$$$ не имеет значения, пока выполняется свойство, указанное в первом предложении.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных. Затем следуют $$$t$$$ наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n \le 100$$$, $$$0 \le k \le n$$$) — половину количества точек и количество хорд, построенных изначально.
Затем следуют $$$k$$$ строк. В $$$i$$$-й из них содержатся два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, \, y_i \le 2n$$$, $$$x_i \ne y_i$$$) — концы $$$i$$$-й хорды. Гарантируется, что $$$2k$$$ чисел $$$x_1, \, y_1, \, x_2, \, y_2, \, \dots, \, x_k, \, y_k$$$ попарно различны.
Для каждого набора входных данных выведите максимальное количество пересечений, которое можно получить, проведя $$$n - k$$$ дополнительных хорд.
4 4 2 8 2 1 5 1 1 2 1 2 0 10 6 14 6 2 20 9 10 13 18 15 12 11 7
4 0 1 14
В первом наборе входных данных, есть три способа нарисовать $$$2$$$ дополнительных хорд, показанных ниже (черные хорды — первоначально нарисованные, а красные — новые):
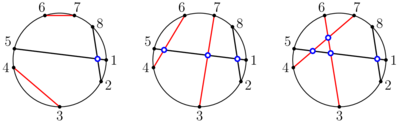
Мы видим, что третий способ дает максимальное количество пересечений, а именно $$$4$$$.
Во втором наборе входных данных, больше не нужно строить хорд. Конечно, при наличии только одной хорды пересечений нет.
В третьем наборе входных данных, мы можем сделать не более одного пересечения, проведя хорды $$$1-3$$$ и $$$2-4$$$, как показано ниже:
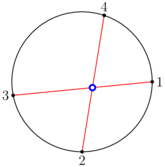
| Название |
|---|




