| Codeforces Round 730 (Div. 2) |
|---|
| Закончено |
В конечном счете вы победили Рэйзора и теперь считаетесь Самым Разыскиваемым уличным гонщиком. Сержант Кросс послал в смертельную погоню за вами целый полицейский отряд. К счастью, вы нашли укромное убежище, но все еще переживаете, что Кросс и его ребята в конце концов вас отыщут. Чтобы увеличить свои шансы на выживание, вы собираетесь перенастроить и перекрасить вашу BMW M3 GTR.
Машину можно представлять как перенумерованный $$$n$$$-мерный гиперкуб. Простым $$$n$$$-мерным гиперкубом называется неориентированный невзвешенный граф, построенный рекурсивно следующим образом:
- Возьмите два простых $$$(n-1)$$$-мерных гиперкуба. Вершины одного из них должны быть пронумерованы числами от $$$0$$$ до $$$2^{n-1}-1$$$, а другого — от $$$2^{n-1}$$$ до $$$2^{n}-1$$$. Простой $$$0$$$-мерный гиперкуб — это одна вершина.
- Добавьте ребро между вершинами $$$i$$$ и $$$i+2^{n-1}$$$ для каждого $$$0\leq i < 2^{n-1}$$$.
Перенумерованный $$$n$$$-мерный гиперкуб получается перестановкой номеров вершин простого $$$n$$$-мерного гиперкуба произвольным образом.
Примеры простого и перенумерованного $$$3$$$-мерных гиперкубов представлены ниже:
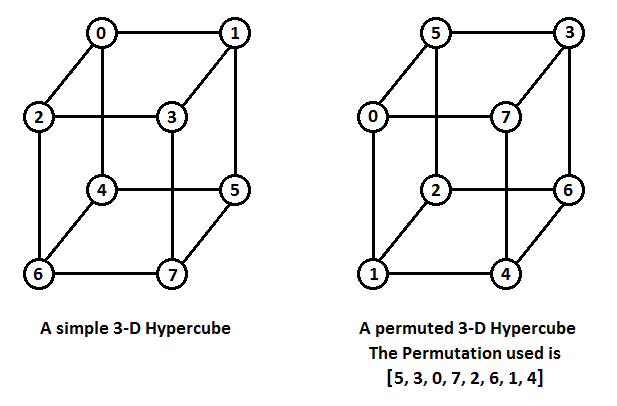
Заметьте, что перенумерованный $$$n$$$-мерный гиперкуб обладает следующими свойствами:
- Он содержит в точности $$$2^n$$$ вершин.
- Он содержит в точности $$$n\cdot 2^{n-1}$$$ ребер.
- Каждая вершина соединена ровно с $$$n$$$ другими вершинами.
- Он не содержит петель и кратных ребер.
Обозначим за $$$P$$$ перестановку, использованную для получения перенумерованного $$$n$$$-мерного гиперкуба, описывающего вашу машину, из простого $$$n$$$-мерного гиперкуба. Прежде чем наводить беспорядок в функциональностях машины, вы хотите найти эту перестановку, чтобы, если что-то пойдет не так, суметь восстановить машину. Но это еще не все.
У вас с собой есть $$$n$$$ различных цветов, пронумерованных от $$$0$$$ до $$$n-1$$$. Вы хотите покрасить вершины перенумерованного $$$n$$$-мерного гиперкуба таким образом, чтобы для каждой вершины $$$u$$$, удовлетворяющей $$$0\leq u < 2^n$$$, и каждого цвета $$$c$$$, удовлетворяющего $$$0\leq c < n$$$, существовала хотя бы одна вершина $$$v$$$, соседняя с $$$u$$$ и покрашенная в цвет $$$c$$$. Иными словами, из каждой вершины должно быть возможно перейти в вершину любого цвета ровно по одному ребру.
Дан перенумерованный $$$n$$$-мерный гиперкуб, найдите любые допустимые перестановку $$$P$$$ и покраску.
Первая строка содержит одно целое число $$$t$$$ ($$$1\leq t\leq 4096$$$) — количество наборов входных данных.
Для каждого набора входных данных первая строка содержит одно целое число $$$n$$$ ($$$1\leq n\leq 16$$$).
Каждая из последующих $$$n\cdot 2^{n-1}$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$0\leq u, v < 2^n$$$), означающее, что вершины $$$u$$$ и $$$v$$$ соединены ребром.
Гарантируется, что граф, описанный во входных данных, задает перенумерованный $$$n$$$-мерный гиперкуб.
Также гарантируется, что сумма $$$2^n$$$ по всем наборам входных данных не превосходит $$$2^{16}=65\,536$$$.
Для каждого набора входных данных выведите две строки.
В первой строке выведите любую перестановку $$$P$$$ длины $$$2^n$$$, которая может быть использована для получения перенумерованного $$$n$$$-мерного гиперкуба, данного во входных данных, из простого $$$n$$$-мерного гиперкуба. Два перенумерованных гиперкуба считаются одинаковыми, если они имеют одинаковый набор ребер. Если возможно несколько ответов, выведите любой из них.
Во второй строке выведите покраску. Если не существует покраски, удовлетворяющей условиям, выведите $$$-1$$$. В противном случае напечатайте одну строку, содержащую $$$2^n$$$ целых чисел, разделенных пробелом. $$$i$$$-е число должно быть равно цвету вершины с номером $$$(i-1)$$$ в перенумерованном $$$n$$$-мерном гиперкубе. Если возможно несколько ответов, выведите любой из них.
3 1 0 1 2 0 1 1 2 2 3 3 0 3 0 1 0 5 0 7 1 2 1 4 2 5 2 6 3 5 3 6 3 7 4 6 4 7
0 1 0 0 0 1 3 2 0 0 1 1 5 3 0 7 2 6 1 4 -1
Покраска и перенумерованный гиперкуб для первого набора входных данных представлены ниже:
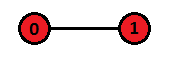
Покраска и перенумерованный гиперкуб для второго набора входных данных представлены ниже:
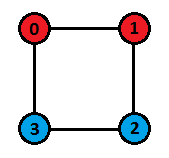
Перенумерованный гиперкуб для третьего набора дан в условии задачи. Однако, можно показать, что не существует покраски, удовлетворяющей всем условиям. Заметьте, что некоторые другие перестановки, например, $$$[0, 5, 7, 3, 1, 2, 4, 6]$$$ и $$$[0, 1, 5, 2, 7, 4, 3, 6]$$$ дадут этот же перенумерованный гиперкуб.
| Название |
|---|




