| Codeforces Round 728 (Div. 1) |
|---|
| Закончено |
Вам задано дерево, состоящее из $$$n$$$ вершин. По заданному дереву вы строите массив, отмечая вершины по одной.
Первоначально, когда еще не помечено ни одной вершины, вы выбираете вершину равновероятно по всем вершинам дерева и отмечаете ее.
После этого, пока еще остаются непомеченные вершины, вы выбираете и помечаете вершину равновероятно среди всех еще непомеченных, но связанных по ребру хотя бы с одной помеченной вершиной.
Можно доказать, что данный процесс пометит все вершины в дереве.
Финальный массив $$$a$$$ — это список номеров вершин в порядке, в котором они были помечены.
Определите математическое ожидание количества инверсий в массиве, полученном на основе заданного дереве с помощью описанного выше алгоритма.
Количество инверсий в массиве $$$a$$$ — это количество пар индексов $$$(i, j)$$$ таких, что $$$i < j$$$ и $$$a_i > a_j$$$. Например, в массиве $$$[4, 1, 3, 2]$$$ количество инверсий равно $$$4$$$: $$$(1, 2)$$$, $$$(1, 3)$$$, $$$(1, 4)$$$, $$$(3, 4)$$$.
В первой строке задано одно целое число $$$n$$$ ($$$2 \le n \le 200$$$) — количество вершин в дереве.
В следующих $$$n - 1$$$ строках заданы по два целых числа $$$x$$$ и $$$y$$$ ($$$1 \le x, y \le n$$$; $$$x \neq y$$$), означающие ребро между вершинами $$$x$$$ и $$$y$$$.
Гарантируется, что заданные ребра образуют дерево.
Выведите математическое ожидание количества инверсий в построенном массиве по модулю $$$10^9+7$$$.
Формально, пусть $$$M = 10^9+7$$$. Можно показать, что ответ может быть представлен в виде несократимой дроби $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ — целые числа, и $$$q \not \equiv 0 \pmod{M}$$$. Выведите целое число, равное $$$p \cdot q^{-1} \bmod M$$$. Другими словами, выведите такое целое число $$$x$$$, что $$$0 \le x < M$$$ и $$$x \cdot q \equiv p \pmod{M}$$$.
3 1 2 1 3
166666669
6 2 1 2 3 6 1 1 4 2 5
500000009
5 1 2 1 3 1 4 2 5
500000007
Изображение дерева из первого примера:
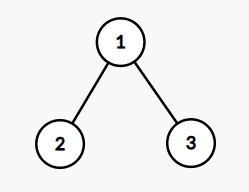
В первом примере получающиеся массивы почти фиксированы. Если первоначально выбрана вершина $$$2$$$, то единственный возможный массив — это $$$[2, 1, 3]$$$ ($$$1$$$ инверсия). Если первоначально выбрана вершина $$$3$$$, то единственный возможный массив — это $$$[3, 1, 2]$$$ ($$$2$$$ инверсии). Если первоначально выбрана вершина $$$1$$$, то массивы $$$[1, 2, 3]$$$ ($$$0$$$ инверсий) и $$$[1, 3, 2]$$$ ($$$1$$$ инверсия) — это единственные варианты и они равновероятны. В результате математическое ожидание количества инверсий равно $$$\frac{1}{3}\cdot 1 + \frac{1}{3} \cdot 2 + \frac{1}{3} \cdot (\frac{1}{2} \cdot 0 + \frac{1}{2} \cdot 1) = \frac{7}{6}$$$.
$$$166666669 \cdot 6 = 7 \pmod {10^9 + 7}$$$, то есть ответ равен $$$166666669$$$.
Изображение дерева из второго примера:
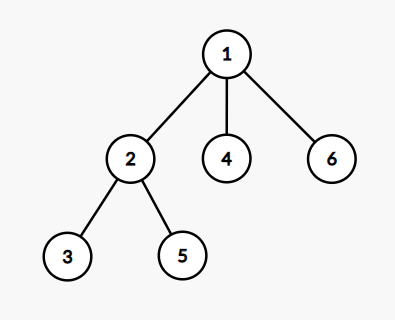
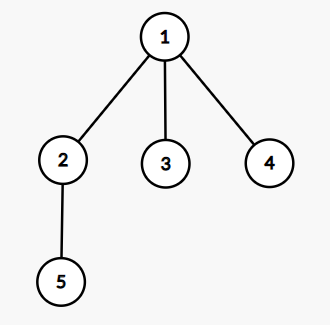
Изображение дерева из третьего примера:
| Название |
|---|




