$$$2^k$$$ команд участвуют в плей-офф турнире. Турнир состоит из $$$2^k - 1$$$ игры. Они проводятся следующим образом: во-первых, команды делятся на пары: команда $$$1$$$ играет против команды $$$2$$$, команда $$$3$$$ играет против команды $$$4$$$ (именно в таком порядке) и так далее (таким образом, в этой фазе будет сыграно $$$2^{k-1}$$$ игры). Когда команда проигрывает игру, она выбывает, и каждая игра приводит к выбыванию одной команды (нет ничьих). После этого остается $$$2^{k-1}$$$ команд. Если остается только одна команда, она объявляется чемпионом; в противном случае играется еще $$$2^{k-2}$$$ игр: в первой из них победитель игры «$$$1$$$ против $$$2$$$» играет против победителя игры «$$$3$$$ против $$$4$$$», затем победитель игры «$$$5$$$ против $$$6$$$» играет против победителя игры «$$$7$$$ против $$$8$$$» и так далее. Этот процесс повторяется до тех пор, пока не останется только одна команда.
Например, на этом рисунке описан хронологический порядок игр с $$$k = 3$$$:
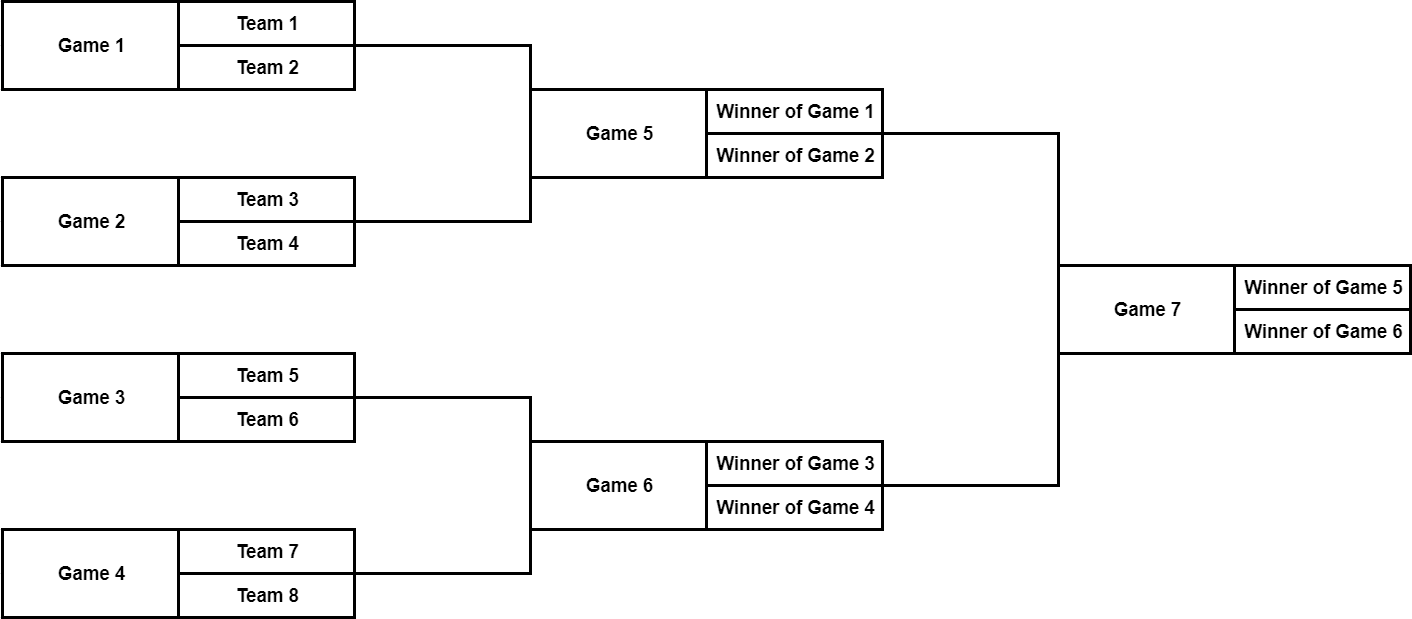
Пусть строка $$$s$$$, состоящая из $$$2^k - 1$$$ символов, описывает результаты игр в хронологическом порядке следующим образом:
- если $$$s_i$$$ равно 0, то команда с меньшим индексом выигрывает $$$i$$$-ю игру;
- если $$$s_i$$$ равно 1, то команда с большим индексом выигрывает $$$i$$$-ю игру;
- если $$$s_i$$$ равно ?, то результат $$$i$$$-й игры неизвестен (любая команда может выиграть эту игру).
Пусть $$$f(s)$$$ — число возможных победителей турнира, описываемого строкой $$$s$$$. Команда $$$i$$$ является возможным победителем турнира, если можно заменить каждый ? на 1 или 0 таким образом, что команда $$$i$$$ является чемпионом.
Вам дается начальное состояние строки $$$s$$$. Вы должны обработать $$$q$$$ запросов следующей формы:
- $$$p$$$ $$$c$$$ — заменить $$$s_p$$$ символом $$$c$$$ и вывести $$$f(s)$$$ в результате запроса.
Первая строка содержит одно целое число $$$k$$$ ($$$1 \le k \le 18$$$).
Вторая строка содержит строку, состоящую из $$$2^k - 1$$$ символов — начальное состояние строки $$$s$$$. Каждый символ либо ?, 0, либо 1.
Третья строка содержит одно целое число $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — количество запросов.
Затем следует $$$q$$$ строк, строка $$$i$$$ содержит целое число $$$p$$$ и символ $$$c$$$ ($$$1 \le p \le 2^k - 1$$$; $$$c$$$ - это либо ?, 0, либо 1), описывающие запрос $$$i$$$.
Для каждого запроса выведите одно целое число — $$$f(s)$$$.
3 0110?11 6 5 1 6 ? 7 ? 1 ? 5 ? 1 1
1 2 3 3 5 4
| Название |
|---|




