| Codeforces Round 722 (Div. 1) |
|---|
| Закончено |
У Parsa есть огромное дерево на $$$n$$$ вершинах.
На каждой вершине $$$v$$$ он записал два целых числа $$$l_v$$$ и $$$r_v$$$.
Чтобы дерево Parsa выглядело еще более величественным, Nima хочет назначить число $$$a_v$$$ ($$$l_v \le a_v \le r_v$$$) для каждой вершины $$$v$$$ таким образом, чтобы красота дерева Parsa была максимальной.
Восприятие красоты Nima довольно причудливо. Он определяет красоту дерева как сумму $$$|a_u - a_v|$$$ по всем ребрам $$$(u, v)$$$ дерева.
Поскольку дерево Parsa слишком велико, Nima не может самостоятельно максимизировать его красоту. Ваша задача — найти максимальную возможную красоту для дерева Parsa.
Первая строка содержит целое число $$$t$$$ $$$(1\le t\le 250)$$$ — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ $$$(2\le n\le 10^5)$$$ — количество вершин в дереве Parsa.
В $$$i$$$-й из следующих $$$n$$$ строк содержится два целых числа $$$l_i$$$ и $$$r_i$$$ $$$(1 \le l_i \le r_i \le 10^9)$$$.
Каждая из следующих $$$n-1$$$ строк содержит по два целых числа $$$u$$$ и $$$v$$$ $$$(1 \le u , v \le n, u\neq v)$$$, что обозначает наличие ребра между вершинами $$$u$$$ и $$$v$$$ в дереве Parsa.
Гарантируется, что данный граф является деревом.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите максимальную возможную красоту для дерева Парса.
3 2 1 6 3 8 1 2 3 1 3 4 6 7 9 1 2 2 3 6 3 14 12 20 12 19 2 12 10 17 3 17 3 2 6 5 1 5 2 6 4 6
7 8 62
Деревья в примере:
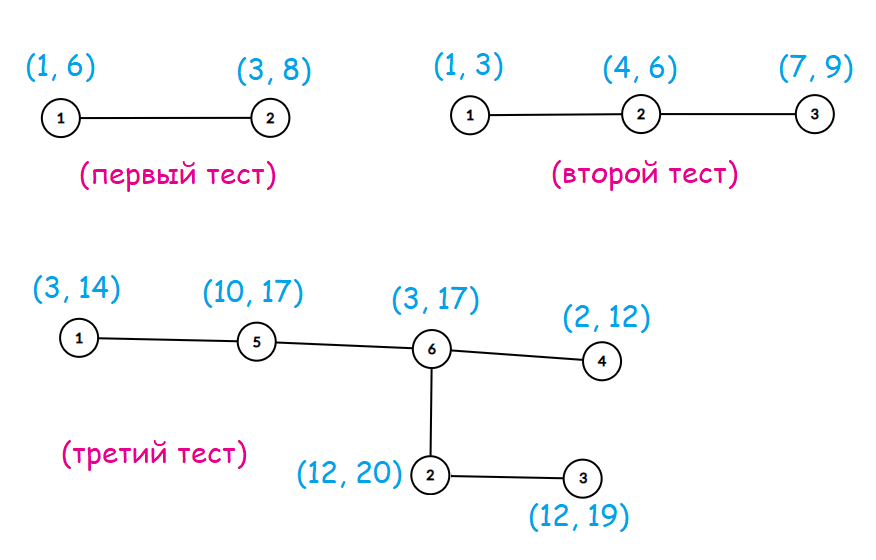
В первом наборе входных данных одно из возможных назначений — $$$a = \{1, 8\}$$$, что приводит к $$$|1 - 8| = 7$$$.
Во втором наборе входных данных одно из возможных назначений — $$$a = \{1, 5, 9\}$$$, что приводит к красоте $$$|1 - 5| + |5 - 9| = 8$$$.
| Название |
|---|




