| Codeforces Round 721 (Div. 2) |
|---|
| Закончено |
Вам дано дерево из $$$n$$$ вершин, в котором вершины пронумерованы от $$$0$$$ до $$$n-1$$$. Для каждого $$$k$$$ от $$$0$$$ до $$$n$$$ включительно вам необходимо посчитать количество неупорядоченных пар $$$(u,v)$$$, $$$u \neq v$$$, таких, что MEX всех номеров вершин на пути от $$$u$$$ до $$$v$$$ равен $$$k$$$.
MEX последовательности целых чисел равен наименьшему неотрицательному целому числу, которое в ней не встречается.
Первая строка содержит целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^{5}$$$).
Следующая $$$n-1$$$ строка содержит описание дерева. Каждая строка содержит два целых числа $$$u$$$ и $$$v$$$ ($$$0 \le u,v \le n-1$$$), задающие ребро между $$$u$$$ и $$$v$$$ ($$$u \neq v$$$).
Гарантируется, что данные ребра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^{5}$$$.
Для каждого набора входных данных выведите $$$n+1$$$ целое число: число путей в дереве таких, что MEX всех номеров вершин на нем равен $$$k$$$, для всех $$$k$$$ от $$$0$$$ до $$$n$$$.
2 4 0 1 0 2 2 3 2 1 0
1 2 1 1 1 0 0 1
- В наборе входных данных $$$1$$$:
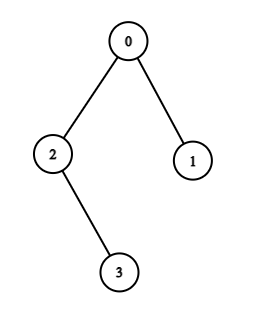
- Для $$$k = 0$$$ существует только $$$1$$$ путь из $$$2$$$ в $$$3$$$ с $$$MEX([2, 3]) = 0$$$.
- Для $$$k = 1$$$ существует $$$2$$$ пути. Один из $$$0$$$ в $$$2$$$ с $$$MEX([0, 2]) = 1$$$, и из $$$0$$$ в $$$3$$$ с $$$MEX([0, 2, 3]) = 1$$$.
- Для $$$k = 2$$$ существует $$$1$$$ путь из $$$0$$$ в $$$1$$$ с $$$MEX([0, 1]) = 2$$$.
- Для $$$k = 3$$$ существует $$$1$$$ путь из $$$1$$$ в $$$2$$$ с $$$MEX([1, 0, 2]) = 3$$$
- Для $$$k = 4$$$ существует $$$1$$$ путь из $$$1$$$ в $$$3$$$ с $$$MEX([1, 0, 2, 3]) = 4$$$.
- В наборе входных данных $$$2$$$:
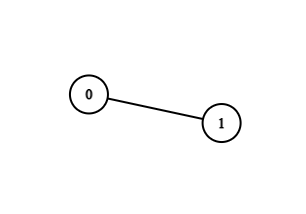
- Для $$$k = 0$$$ не существует таких путей.
- Для $$$k = 1$$$ не существует таких путей.
- Для $$$k = 2$$$ существует $$$1$$$ путь из $$$0$$$ в $$$1$$$ с $$$MEX([0, 1]) = 2$$$.
| Название |
|---|




