
Василий — большой любитель планирования дел наперед. Поэтому каждое утро он занимается формированием вложенного списка предстоящих дел.
Корректным вложенным списком является любой список, который можно получить из списка с одним пунктом «1» путем применения операций. Каждая операция вставляет в список новый пункт на следующей строке после одного из уже существующих пунктов $$$a_1 \,.\, a_2 \,.\, a_3 \,.\, \,\cdots\, \,.\,a_k$$$, и бывает двух видов:
- добавить пункт $$$a_1 \,.\, a_2 \,.\, a_3 \,.\, \cdots \,.\, a_k \,.\, 1$$$ (начав более вложенный список), или
- добавить пункт $$$a_1 \,.\, a_2 \,.\, a_3 \,.\, \cdots \,.\, (a_k + 1)$$$ (продолжив текущий уровень).
Когда Василий захотел сохранить Word-документ со списком своих дел, он промахнулся и вместо «Ctrl+S» нажал совсем другую комбинацию клавиш. Достоверно неизвестно, что это была за комбинация клавиш, но после ее нажатия каждый пункт списка заменился одним числом: числом, изначально написанным последним в номере пункта.
Василий хочет, чтобы вы помогли ему восстановить подходящий изначальный вложенный список.
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка набора входных данных содержит целое число $$$n$$$ ($$$1 \le n \le 10^3$$$) — количество строк в списке.
Следующие $$$n$$$ строк набора входных данных содержат по одному числу $$$a_i$$$ ($$$1 \le a_i \le n$$$) — описание того, что осталось от вложенного списка Василия.
Гарантируется, что в каждом наборе входных данных существует хотя бы один подходящий список.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^3$$$.
Для каждого набора входных данных выведите $$$n$$$ строк, которые являются корректным вложенным списком, из которого мог получиться список, который вам предоставил Василий.
Если ответов несколько, то вы можете вывести любой подходящий.
2 4 1 1 2 3 9 1 1 1 2 2 1 2 1 2
1 1.1 1.2 1.3 1 1.1 1.1.1 1.1.2 1.2 1.2.1 2 2.1 2.2
Во втором наборе входных данных одним из корректных подходящих списков является:
1
1.1
1.1.1
1.1.2
1.2
1.2.1
2
2.1
2.2
Такой список можно получить при помощи последовательности операций, показанной ниже: 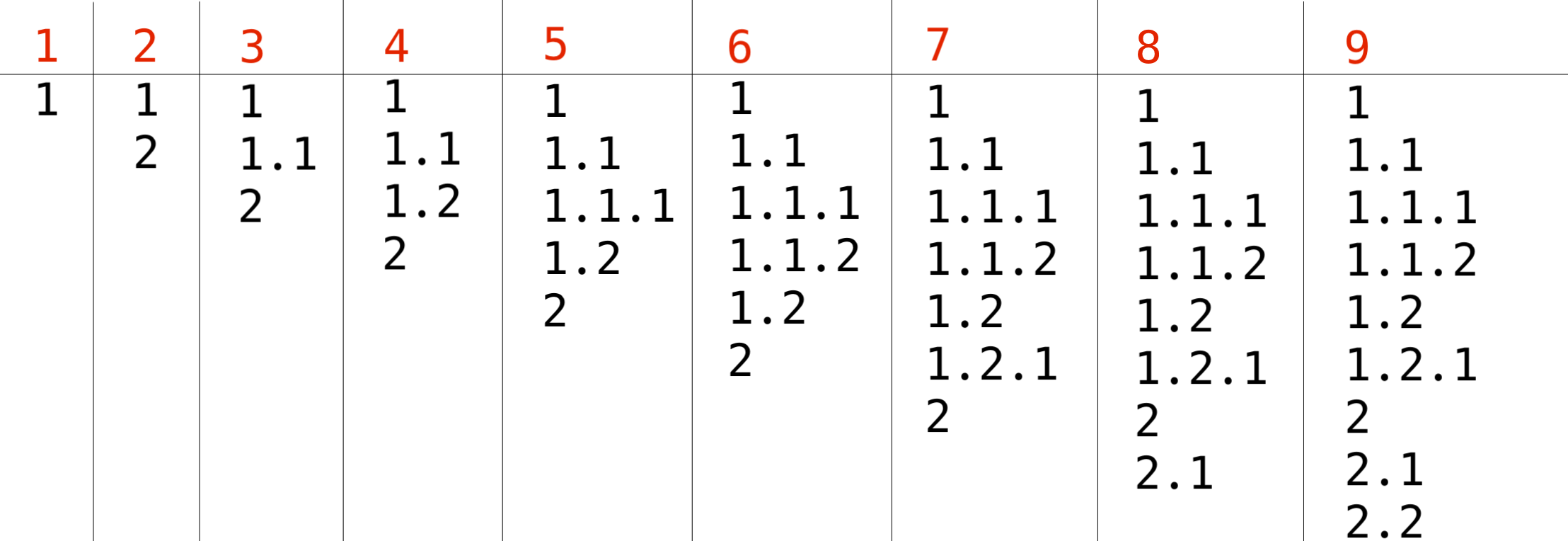
- Изначальный список с одним пунктом $$$1$$$.
- Вставляем пункт $$$2$$$ при помощи операции вставки второго типа после пункта $$$1$$$.
- Вставляем пункт $$$1.1$$$ при помощи операции вставки первого типа после пункта $$$1$$$.
- Вставляем пункт $$$1.2$$$ при помощи операции вставки второго типа после пункта $$$1.1$$$.
- Вставляем пункт $$$1.1.1$$$ при помощи операции вставки первого типа после пункта $$$1.1$$$.
- Вставляем пункт $$$1.1.2$$$ при помощи операции вставки второго типа после пункта $$$1.1.1$$$.
- Вставляем пункт $$$1.2.1$$$ при помощи операции вставки первого типа после пункта $$$1.2$$$.
- Вставляем пункт $$$2.1$$$ при помощи операции вставки первого типа после пункта $$$2$$$.
- Вставляем пункт $$$2.2$$$ при помощи операции вставки второго типа после пункта $$$2.1$$$.
| Название |
|---|




