| Codeforces Round 720 (Div. 2) |
|---|
| Закончено |
У Насти есть невзвешенное дерево из $$$n$$$ вершин, с которым ей не терпится поиграть!
Девочка будет выполнять следующую операцию с деревом столько раз, сколько ей потребуется:
- удалить любое существующее ребро, затем
- добавить неориентированное ребро между любой парой вершин.
Какое минимальное количество операций требуется девочке, чтобы получить из дерева бамбук? Бамбуком называется дерево, степень вершин в котором не превосходит $$$2$$$.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10\,000$$$) — количество наборов входных данных.
В первой строке каждого набора задано число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество вершин в дереве.
Следующая $$$n - 1$$$ строка каждого набора входных данных описывают ребро дерево в формате $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$, $$$a_i \neq b_i$$$).
Гарантируется, что заданный граф является деревом и сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого из наборов входных данных в первой строке выведите одно целое число $$$k$$$ — минимальное количество операций, необходимых, чтобы получить из дерева бамбук.
В последующих $$$k$$$ строках выведите $$$4$$$ целых числа $$$x_1$$$, $$$y_1$$$, $$$x_2$$$, $$$y_2$$$ ($$$1 \le x_1, y_1, x_2, y_{2} \le n$$$, $$$x_1 \neq y_1$$$, $$$x_2 \neq y_2$$$) — таким образом вы удаляете ребро $$$(x_1, y_1)$$$ и добавляете неориентированное ребро $$$(x_2, y_2)$$$.
Обратите внимание, что ребро $$$(x_1, y_1)$$$ обязано содержаться в графе до его удаления.
2 7 1 2 1 3 2 4 2 5 3 6 3 7 4 1 2 1 3 3 4
2 2 5 6 7 3 6 4 5 0
Обратите внимание, что граф может быть несвязным после какого-то количества операций.
Рассмотрим первый набор входных данных:
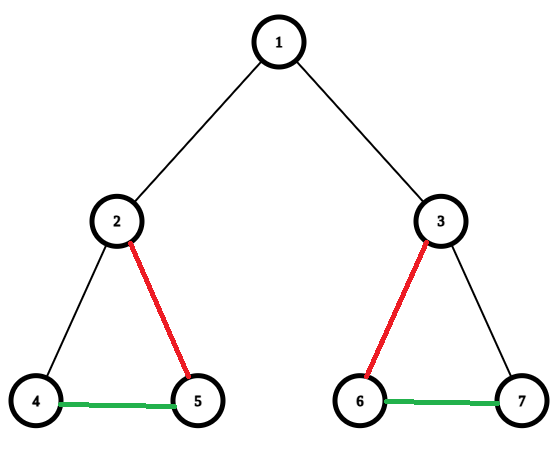
| Название |
|---|




