На бесконечной плоскости лежат $$$n$$$ точек. Координаты $$$i$$$-й точки $$$(x_i, y_i)$$$ такие, что $$$x_i > 0$$$ и $$$y_i > 0$$$. Координаты необязательно целые.
За один ход осуществляются следующие операции:
- выбрать две точки $$$a$$$ и $$$b$$$ ($$$a \neq b$$$);
- подвинуть точку $$$a$$$ из $$$(x_a, y_a)$$$ либо в $$$(x_a + 1, y_a)$$$, либо в $$$(x_a, y_a + 1)$$$;
- подвинуть точку $$$b$$$ из $$$(x_b, y_b)$$$ либо в $$$(x_b + 1, y_b)$$$, либо в $$$(x_b, y_b + 1)$$$;
- удалить точки $$$a$$$ и $$$b$$$.
Ход можно совершить только в том случае, если существует прямая, проходящая через новые координаты $$$a$$$, новые координаты $$$b$$$ и $$$(0, 0)$$$.
Иначе ход совершить нельзя, и точки остаются на своих начальных координатах $$$(x_a, y_a)$$$ и $$$(x_b, y_b)$$$, соответственно.
Нумерация точек не меняется после удаления точек. Если точки удалены, то они не могут быть выбраны в последующих ходах. Обратите внимание, что необходимо двигать обе точки во время хода, нельзя оставлять их в изначальных координатах.
Какое наибольшее количество ходов можно совершить? Какие это ходы?
Если существует несколько ответов, то выведите любой из них.
В первой строке записано одно целое $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество точек.
В $$$i$$$-й из следующих $$$n$$$ строк записаны четыре целых числа $$$a_i, b_i, c_i, d_i$$$ ($$$1 \le a_i, b_i, c_i, d_i \le 10^9$$$). Координаты $$$i$$$-й точки — $$$x_i = \frac{a_i}{b_i}$$$ и $$$y_i = \frac{c_i}{d_i}$$$.
В первой строке выведите одно целое число $$$c$$$ — наибольшее количество ходов, которые можно совершить.
В каждой из следующих $$$c$$$ строк должно быть записано описание хода: два целых числа $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le n$$$, $$$a \neq b$$$) — точки, удаляемые на текущем ходу. Должен существовать способ подвинуть точки $$$a$$$ и $$$b$$$ согласно условию так, чтобы существовала прямая, проходящая через новые координаты $$$a$$$, новые координаты $$$b$$$ и $$$(0, 0)$$$. Никакая удаленная точка не может быть удалена в последующих ходах.
Если существует несколько ответов, то выведите любой из них. Можно выводить ходы и точки внутри ходов в произвольном порядке.
7 4 1 5 1 1 1 1 1 3 3 3 3 1 1 4 1 6 1 1 1 5 1 4 1 6 1 1 1
3 1 6 2 4 5 7
4 2 1 1 1 1 1 2 1 2 1 1 2 1 2 1 2
1 1 2
4 182 168 60 96 78 72 45 72 69 21 144 63 148 12 105 6
1 2 4
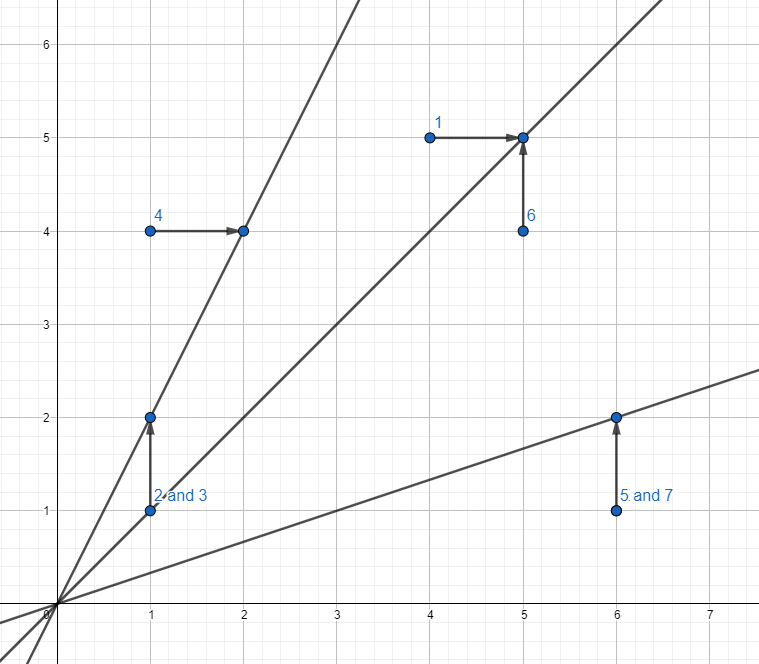
Точки из первого примера и перемещения для тех из них, которые выбираются в ходах:
| Название |
|---|




