У подножия горы Лиюшань будут установлены $$$n$$$ палаток, для тех, кто желает испытать радость от единения с природой, спокойствия ночи и яркого звездного неба.
Палатка номер $$$i$$$ будет расположена в точке $$$(x_i, y_i)$$$ и будет иметь вес $$$w_i$$$. Палатка считается важной, если оба $$$x_i$$$ и $$$y_i$$$ являются четными. Вам нужно убрать некоторые из палаток так, чтобы для каждой оставшейся важной палатки $$$(x, y)$$$ не существовало $$$3$$$ другие палатки $$$(x'_1, y'_1)$$$, $$$(x'_2, y'_2)$$$ и $$$(x'_3, y'_3)$$$, такие что оба условия выполнены:
- $$$|x'_j-x|, |y'_j - y|\leq 1$$$ для всех $$$j \in \{1, 2, 3\}$$$.
- Эти четыре палатки образуют параллелограмм (или прямоугольник), и одна из его сторон параллельна оси $$$x$$$.
Максимизируйте сумму весов оставшихся палаток.
Первая строка содержит одно целое число $$$n$$$ ($$$1\leq n\leq 1\,000$$$), обозначающее количество палаток.
Каждая из следующих $$$n$$$ строк содержит три целых числа $$$x_i$$$, $$$y_i$$$ и $$$w_i$$$ ($$$-10^9\leq x_i,y_i \leq 10^9$$$, $$$1\leq w_i\leq 10^9$$$), обозначающие координаты $$$i$$$-й палатки и ее вес. Никакие две палатки не расположены в одной точке.
Выведите одно целое число — максимальную сумму весов оставшихся палаток.
5 0 0 4 0 1 5 1 0 3 1 1 1 -1 1 2
12
32 2 2 1 2 3 1 3 2 1 3 3 1 2 6 1 2 5 1 3 6 1 3 5 1 2 8 1 2 9 1 1 8 1 1 9 1 2 12 1 2 11 1 1 12 1 1 11 1 6 2 1 7 2 1 6 3 1 5 3 1 6 6 1 7 6 1 5 5 1 6 5 1 6 8 1 5 8 1 6 9 1 7 9 1 6 12 1 5 12 1 6 11 1 7 11 1
24
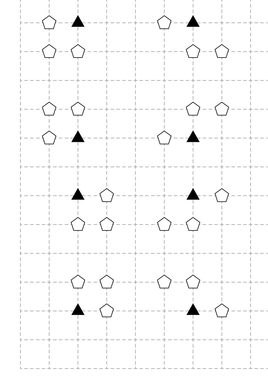
Иллюстрация для второго примера. Черные треугольники обозначают важные палатки. Этот пример также показывает все $$$8$$$ запрещенных паттернов.
| Название |
|---|




