Филломино это классическая головоломка. (Вам не нужно знать Филломино, чтобы решить эту задачу.) В одной из аудиторий в городе Юньци несколько человек играют в настольную игру, вдохновленную этой головоломкой:
Рассмотрим шахматную доску $$$n$$$ на $$$n$$$. Ее строки пронумерованы от $$$1$$$ до $$$n$$$ сверху вниз. А столбцы пронумерованы от $$$1$$$ до $$$n$$$ слева направо. Клетка на пересечении $$$x$$$-й строки и $$$y$$$-го столбца обозначается $$$(x, y)$$$. Главная диагональ доски это клетки $$$(x, x)$$$ для всех $$$1 \le x \le n$$$.
На главной диагонали доски написана перестановка чисел $$$\{1, 2, 3, \dots, n\}$$$. В каждой из клеток написано ровно одно число. Цель игры — разделить клетки ниже и на главной диагонали (таких клеток ровно $$$1+2+ \ldots +n$$$ штук) на $$$n$$$ связных областей, которые удовлетворяют следующим условиям:
- Каждая область должна быть связной. Это означает, что мы можем добраться от любой клетки области до любой другой клетки той же области, посещая только клетки из этой области и перемещаясь из клетки в соседнюю по стороне.
- $$$x$$$-я область должна содержать клетку главной диагонали, в которой написано $$$x$$$, для всех $$$1\le x\le n$$$.
- Количество клеток, принадлежащих $$$x$$$-й области, должно равняться $$$x$$$ для всех $$$1\le x\le n$$$.
- Каждая клетка ниже и на главной диагонали должна принадлежать ровно одной области.
Первая строка содержит одно целое число $$$n$$$ ($$$1\le n \le 500$$$), обозначающее размер доски.
Вторая строка содержит $$$n$$$ целых чисел $$$p_1$$$, $$$p_2$$$, ..., $$$p_n$$$. $$$p_i$$$ это число, написанное в клетке $$$(i, i)$$$. Гарантируется, что каждое из чисел $$$\{1, \ldots, n\}$$$ встречаются ровно один раз среди $$$p_1$$$, ..., $$$p_n$$$.
Если решения не существует, выведите $$$-1$$$.
Иначе, выведите $$$n$$$ строк. $$$i$$$-я строка должна содержать $$$i$$$ чисел. $$$j$$$-е число в $$$i$$$-й строке должно равняться $$$x$$$, если клетка $$$(i, j)$$$ принадлежит области размера $$$x$$$.
3 2 3 1
2 2 3 3 3 1
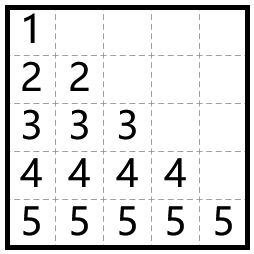
5 1 2 3 4 5
1 2 2 3 3 3 4 4 4 4 5 5 5 5 5
Решения для примеров изображены на иллюстрациях: 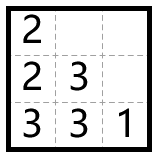
| Название |
|---|




