Вам дан массив $$$a$$$ из $$$n$$$ ($$$n \geq 2$$$) положительных целых чисел, а также целое число $$$p$$$. Рассмотрим неориентированный взвешенный граф на $$$n$$$ вершинах, пронумерованных от $$$1$$$ до $$$n$$$, в котором между вершинами $$$i$$$ и $$$j$$$ ($$$i<j$$$) добавлены следующие ребра:
- Если $$$gcd(a_i, a_{i+1}, a_{i+2}, \dots, a_{j}) = min(a_i, a_{i+1}, a_{i+2}, \dots, a_j)$$$, то между вершинами $$$i$$$ и $$$j$$$ существует ребро веса $$$min(a_i, a_{i+1}, a_{i+2}, \dots, a_j)$$$.
- Если $$$i+1=j$$$, то между вершинами $$$i$$$ и $$$j$$$ существует ребро веса $$$p$$$.
Здесь $$$gcd(x, y, \ldots)$$$ обозначает наибольший общий делитель (НОД) чисел $$$x$$$, $$$y$$$, ....
Обратите внимание, между вершинами $$$i$$$ и $$$j$$$ появляются кратные ребра, если оба условия выполнены. Если же ни одно условие не выполнено для $$$i$$$ и $$$j$$$, то между ними нет ребер.
Ваша цель — найти вес минимального остовного дерева данного графа.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$p$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$, $$$1 \leq p \leq 10^9$$$) — количество вершин и параметр $$$p$$$.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, a_3, \dots, a_n$$$ ($$$1 \leq a_i \leq 10^9$$$).
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Выведите $$$t$$$ строк. Для каждого набора входных данных выведите вес соответствующего минимального остовного дерева.
4 2 5 10 10 2 5 3 3 4 5 5 2 4 9 8 8 5 3 3 6 10 100 9 15
5 3 12 46
Ниже изображены графы для четырех наборов входных данных примера (ребра одного из минимальных остовных деревьев показаны розовым):
Набор 1
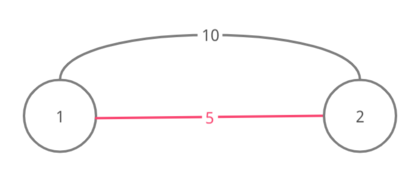
Набор 2
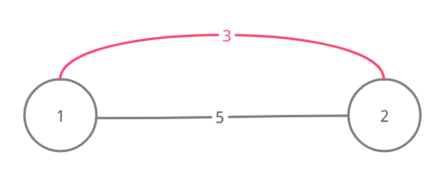
Набор 3
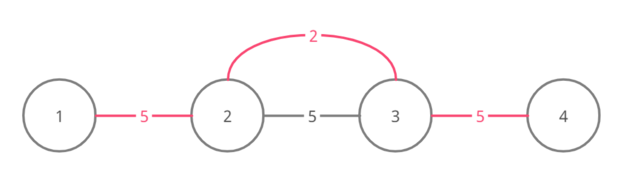
Набор 4
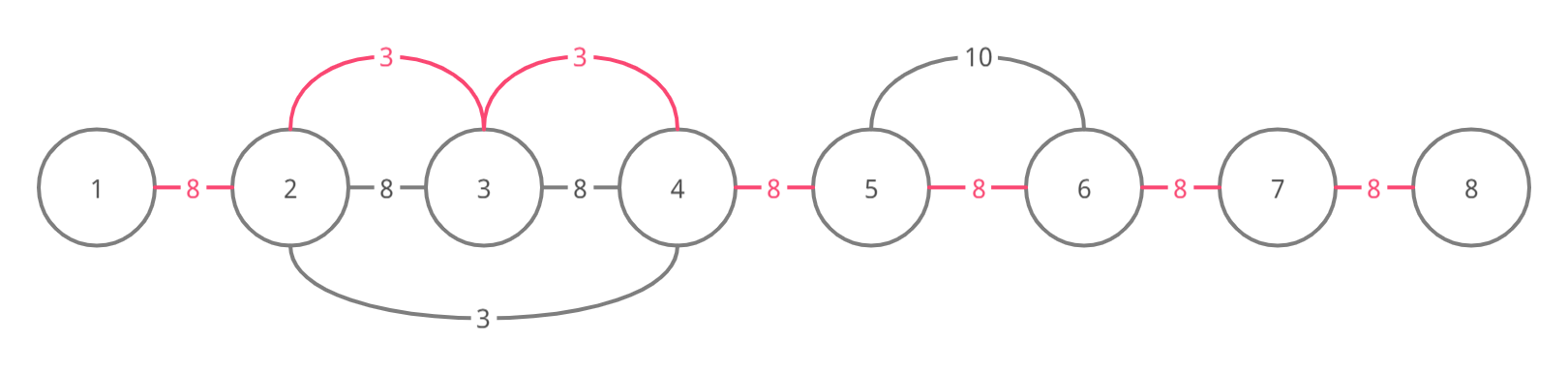
| Название |
|---|




