| Codeforces Round 715 (Div. 1) |
|---|
| Закончено |
В связи со специфическим инцидентом на баскетбольной тренировке, Akari придумал следующую задачу со спортивного программирования!
Вам даны $$$n$$$ точек на плоскости, никакие три из которых не лежат на одной прямой. Изначально точка $$$i$$$ имеет метку $$$a_i$$$, причем метки $$$a_1, a_2, \dots, a_n$$$ образуют перестановку чисел $$$1, 2, \dots, n$$$.
Вы можете менять эти метки с помощью следующей операции:
- Выберите два разных целых числа $$$i$$$ и $$$j$$$ между $$$1$$$ и $$$n$$$.
- Поменяйте местами метки точек $$$i$$$ и $$$j$$$.
- Нарисуйте отрезок между точками $$$i$$$ и $$$j$$$.
Последовательность операций корректна, если после применения всех операций в последовательности точка $$$k$$$ имеет метку $$$k$$$ для всех $$$k$$$ от $$$1$$$ до $$$n$$$ включительно, и нарисованные отрезки не пересекаются внутри друг друга. Формально, если два отрезка пересекаются, то они должны сделать это в общей конечной точке обоих отрезков.
В частности, все нарисованные отрезки должны быть попарно различными.
Найдите любую корректную последовательность операций или определите, что ее нет.
В первой строке содержится целое число $$$n$$$ ($$$3 \le n \le 2000$$$) — количество точек.
В $$$i$$$-й из следующих $$$n$$$ строк содержится три целых числа $$$x_i$$$, $$$y_i$$$, $$$a_i$$$ ($$$-10^6 \le x_i, y_i \le 10^6$$$, $$$1 \le a_i \le n$$$), что означает, что точка $$$i$$$ имеет координаты $$$(x_i, y_i)$$$ и изначально имеет метку $$$a_i$$$.
Гарантируется, что все точки различны, никакие три точки не лежат на одной прямой, а метки $$$a_1, a_2, \dots, a_n$$$ образуют перестановку чисел $$$1, 2, \dots, n$$$.
Если невозможно выполнить корректную последовательность операций, выведите $$$-1$$$.
В противном случае выведите целое число $$$k$$$ ($$$0 \le k \le \frac{n(n - 1)}{2}$$$) — количество выполняемых операций, а затем $$$k$$$ строк, каждая из которых содержит два целых числа $$$i$$$ и $$$j$$$ ($$$1 \le i, j \le n$$$, $$$i\neq j$$$) — номера точек, выбранных для операции.
Обратите внимание, что вам не требуется минимизировать или максимизировать значение $$$k$$$.
Если возможных ответов несколько, вы можете вывести любой из них.
5 -1 -2 2 3 0 5 1 3 4 4 -3 3 5 2 1
5 1 2 5 3 4 5 1 5 1 3
3 5 4 1 0 0 2 -3 -2 3
0
Следующая анимация демонстрирует первый пример. Черные числа обозначают номера точек, а оранжевые — их метки.
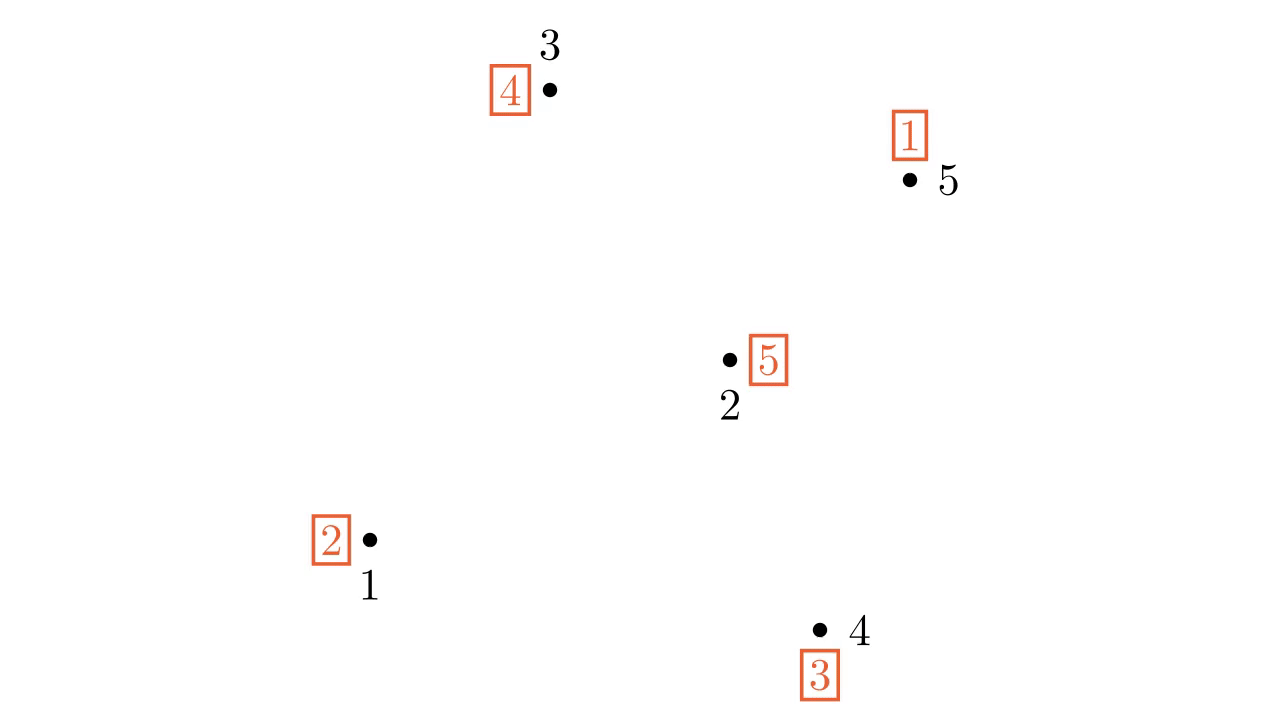
Во втором примере все метки изначально находятся в правильном положении, поэтому никаких операций не требуется.
| Название |
|---|




