Гауранг вырос в таинственной вселенной. Перед ним стоят $$$n$$$ 2D плоскостей одна за другой. Он пускает частицу с периодом распада $$$k$$$ в направлении плоскостей.
Частица может пройти через плоскость напрямую, однако, каждая плоскость создает идентичную копию этой частицы, направленную в противоположном направлении с периодом распада равным $$$k-1$$$. Если период распада частицы равен $$$1$$$, то она НЕ создаст копию.
Например, если есть две плоскости, и выпущена частица с периодом распада $$$3$$$ (направлена вправо), то происходит следующий процесс: (здесь $$$D(x)$$$ означает одну частицу с периодом распада $$$x$$$)
- первая плоскость создает $$$D(2)$$$ влево и пропускает $$$D(3)$$$ дальше вправо;
- вторая плоскость создает $$$D(2)$$$ влево и пропускает $$$D(3)$$$ дальше вправо;
- первая плоскость пропускает $$$D(2)$$$ дальше влево и создает $$$D(1)$$$ вправо;
- вторая плоскость пропускает $$$D(1)$$$ дальше вправо ($$$D(1)$$$ не может создавать копии).
В конце мультимножество $$$S$$$ всех частиц — это $$$\{D(3), D(2), D(2), D(1)\}$$$. (Смотрите примеры для визуального отображения этого теста.)
Гауранг не справляется со сложностью этого процесса, когда количество плоскостей слишком велико. Помогите Гаурангу узнать размер мультимножества $$$S$$$ по заданным $$$n$$$ и $$$k$$$.
Так как размер мультимножества может быть очень большим, выведите его по модулю $$$10^9+7$$$.
Обратите внимание, что частицы могут перемещаться между плоскостями, не сталкиваясь друг с другом.
В первой строке записано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 100$$$). Затем следуют $$$t$$$ строк, в каждой записаны два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n, k \le 1000$$$).
Сумма $$$n$$$ по всем наборам входных данных не превосходит $$$1000$$$. Сумма $$$k$$$ по всем наборам входных данных не превосходит $$$1000$$$. Все наборы входных данных в одном тесте различны.
Выведите $$$t$$$ целых чисел. $$$i$$$-е число должно являться ответом на $$$i$$$-й набор входных данных.
4 2 3 2 2 3 1 1 3
4 3 1 2
3 1 1 1 500 500 250
1 2 257950823
Здесь следует объяснение первого примера, состоящего из четырех наборов входных данных.
Набор входных данных 1: ($$$n = 2$$$, $$$k = 3$$$) уже объяснен в условии задачи.
На картинке ниже изображена симуляция. Каждая цветная прямая показывает путь одной из частиц. Как можно видеть, всего есть четыре различных частицы в мультимножестве. Обратите внимание, что вертикальные промежутки между отраженными частицами введены только для визуальной ясности (как ранее описывалось, частицы не сталкиваются друг с другом)
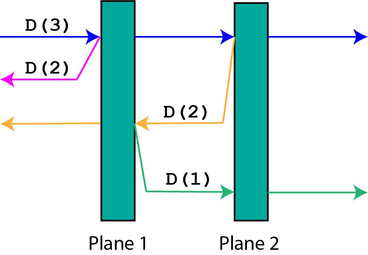
Набор входных данных 2: ($$$n = 2$$$, $$$k = 2$$$) выглядит так:
- первая плоскость создает $$$D(1)$$$ влево и пропускает $$$D(2)$$$ дальше вправо;
- вторая плоскость создает $$$D(1)$$$ влево и пропускает $$$D(2)$$$ дальше вправо;
- первая плоскость пропускает $$$D(1)$$$ дальше влево ($$$D(1)$$$ не может создавать копии).
Итоговый размер мультимножества $$$\{D(1), D(1), D(2)\}$$$ равен трем.
Набор входных данных 3: ($$$n = 3$$$, $$$k = 1$$$) — здесь есть три плоскости, но период распада всего один. Поэтому новые копии не создаются, когда одна частица пролетает через плоскости. Поэтому ответ один.
Набор входных данных 4: ($$$n = 1$$$, $$$k = 3$$$) — здесь только одна плоскость. Частица создает новую копию влево. Мультимножество $$$\{D(2), D(3)\}$$$ имеет размер два.
| Название |
|---|




