У вас есть $$$n$$$ прямоугольников, каждый имеет высоту $$$1$$$. Ширина каждого прямоугольника — степень числа $$$2$$$ (т. е. ее можно представить как $$$2^x$$$ для некоторого неотрицательного целого $$$x$$$).
У вас также есть двумерная коробка ширины $$$W$$$. Обратите внимание, что $$$W$$$ может быть степенью числа $$$2$$$, а может и не быть. Точно известно, что $$$W$$$ не меньше ширины наибольшего прямоугольника.
Вы должны выбрать высоту этой коробки так, чтобы в нее можно было поместить все прямоугольники (при этом высоту необходимо минимизировать). Разрешается укладывать прямоугольники так, чтобы они не занимали все пространство коробки.
Прямоугольники нельзя вращать, кроме того, они не должны пересекаться после укладки (то есть для каждой пары прямоугольников, уложенных в коробку, их площадь пересечения должна быть нулевой).
Посмотрите пояснение для того, чтобы увидеть визуализацию условия задачи.
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 5 \cdot 10^3$$$) — количество наборов входных данных. Каждый набор входных данных состоит из двух строк.
Для каждого набора:
- первая строка содержит два целых числа $$$n$$$ ($$$1 \le n \le 10^5$$$) и $$$W$$$ ($$$1 \le W \le 10^9$$$);
- вторая строка содержит $$$n$$$ целых чисел $$$w_1, w_2, \dots, w_n$$$ ($$$1 \le w_i \le 10^6$$$), где $$$w_i$$$ — ширина $$$i$$$-го прямоугольника. Каждое число $$$w_i$$$ является степенью числа $$$2$$$;
- дополнительное ограничение: $$$\max\limits_{i=1}^{n} w_i \le W$$$.
Сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Выведите $$$t$$$ целых чисел. $$$i$$$-е число должно быть равно ответу на $$$i$$$-й набор входных — минимальной высоте коробки.
2 5 16 1 2 8 4 8 6 10 2 8 8 2 2 8
2 3
Первый набор входных данных в примере разобран на следующей картинке:
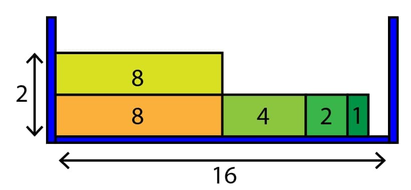
На этой картинке число внутри каждого прямоугольника — это его ширина. Ширина коробки равна $$$16$$$ (см. обозначения в нижней части картинки). Минимальная высота коробки равна $$$2$$$ (см. обозначения в левой части картинки).
Во втором наборе входных данных можно расположить на каждом уровне по одному прямоугольнику ширины 8 и ширины 2, так потребуется всего три уровня (и высота коробки будет равна 3).
| Название |
|---|




