| Codeforces Round 702 (Div. 3) |
|---|
| Закончено |
Перестановка — это последовательность длины $$$n$$$ целых чисел от $$$1$$$ до $$$n$$$, в которой все числа встречаются ровно по одному разу. Например, $$$[1]$$$, $$$[3, 5, 2, 1, 4]$$$, $$$[1, 3, 2]$$$ — перестановки, а $$$[2, 3, 2]$$$, $$$[4, 3, 1]$$$, $$$[0]$$$ — нет.
Поликарпу недавно подарили перестановку $$$a[1 \dots n]$$$ длины $$$n$$$. Поликарпу деревья нравятся больше, чем перестановки, поэтому он хочет превратить перестановку $$$a$$$ в корневое бинарное дерево. Массив различных целых чисел он превращает в дерево следующим образом:
- максимальный элемент массива становится корнем дерева;
- все элементы слева от максимума — образуют левое поддерево (которое строится по тем же правилам, но применяемым для левого участка массива), но если слева от максимума элементов нет, то у корня нет левого сына;
- все элементы справа от максимума — образуют правое поддерево (которое строится по тем же правилам, но применяемым для правого участка массива), но если справа от максимума элементов нет, то у корня нет правого сына.
Например, если он строит дерево по перестановке $$$a=[3, 5, 2, 1, 4]$$$, то корнем будет элемент $$$a_2=5$$$, левым поддеревом будет дерево, которое будет построено для подмассива $$$a[1 \dots 1] = [3]$$$, а правым — для подмассива $$$a[3 \dots 5] = [2, 1, 4]$$$. В итоге будет построено следующее дерево:
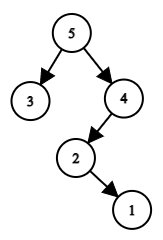 Дерево, соответствующее перестановке $$$a=[3, 5, 2, 1, 4]$$$.
Дерево, соответствующее перестановке $$$a=[3, 5, 2, 1, 4]$$$. Другой пример: пусть перестановка имеет вид $$$a=[1, 3, 2, 7, 5, 6, 4]$$$. В этом случае дерево выглядит так:
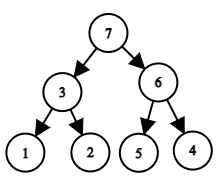 Дерево, соответствующее перестановке $$$a=[1, 3, 2, 7, 5, 6, 4]$$$.
Дерево, соответствующее перестановке $$$a=[1, 3, 2, 7, 5, 6, 4]$$$. Обозначим за $$$d_v$$$ глубину вершины $$$a_v$$$, то есть количество ребер на пути от корня до вершины с номером $$$a_v$$$. Заметьте, что глубина корня равна нулю. По заданной перестановке $$$a$$$ для каждой вершины найдите значение $$$d_v$$$.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных. Далее следуют $$$t$$$ наборов входных данных.
Первая строка каждого набора входных данных содержит целое число $$$n$$$ ($$$1 \le n \le 100$$$) – длину перестановки.
Далее следуют $$$n$$$ различных целых чисел $$$a_1, a_2, \ldots, a_n$$$ — перестановка $$$a$$$.
Для каждого набор входных данных выведите $$$n$$$ значений — $$$d_1, d_2, \ldots, d_n$$$.
3 5 3 5 2 1 4 1 1 4 4 3 1 2
1 0 2 3 1 0 0 1 3 2
| Название |
|---|




