| Codeforces Round 703 (Div. 2) |
|---|
| Закончено |
В стране $$$n$$$ городов и $$$m$$$ двунаправленных дорог. Дороги в стране формируют неориентированный взвешенный граф. Граф может быть несвязным. У каждой дороги есть свой параметр $$$w$$$. Вы можете ездить по дорогам, но правительство издало новый закон: вы можете проезжать только по двум дорогам сразу (проехать из города $$$a$$$ в город $$$b$$$, и из города $$$b$$$ в город $$$c$$$) и вы должны будете заплатить $$$(w_{ab} + w_{bc})^2$$$ денег, чтобы проехать по этим дорогам. Для каждого города $$$t$$$ найдите, можно ли добраться до него из города $$$1$$$, и какое наименьшее количество денег необходимо потратить, чтобы добраться из $$$1$$$ в $$$t$$$.
В первой строке находятся два целых числа $$$n$$$, $$$m$$$ ($$$2 \leq n \leq 10^5$$$, $$$1 \leq m \leq min(\frac{n \cdot (n - 1)}{2}, 2 \cdot 10^5)$$$).
В следующих $$$m$$$ строках находятся по три целых числа $$$v_i$$$, $$$u_i$$$, $$$w_i$$$ ($$$1 \leq v_i, u_i \leq n$$$, $$$1 \leq w_i \leq 50$$$, $$$u_i \neq v_i$$$). Гарантируется, что в графе нет кратных рёбер, то есть для любого ребра $$$(u_i, v_i)$$$ не существует других рёбер $$$(u_i, v_i)$$$ или $$$(v_i, u_i)$$$.
Для каждого города $$$t$$$ выведите одно целое число. Если нет корректного пути из $$$1$$$ в $$$t$$$ выведите $$$-1$$$. Иначе выведите минимальное необходимое количество денег, чтобы добраться из $$$1$$$ в $$$t$$$.
5 6 1 2 3 2 3 4 3 4 5 4 5 6 1 5 1 2 4 2
0 98 49 25 114
3 2 1 2 1 2 3 2
0 -1 9
Граф в первом примере выглядит так.
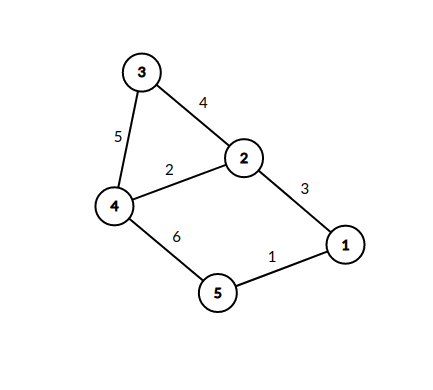
Во втором примере путь из $$$1$$$ в $$$3$$$ проходит через $$$2$$$, так что результирующая стоимость поездки будет $$$(1 + 2)^2 = 9$$$.
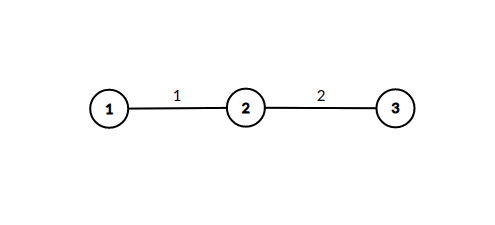
| Название |
|---|




