| Codeforces Round 699 (Div. 2) |
|---|
| Закончено |
Kilani и Abd — соседи уже на протяжении 3000 лет, но пришел день и Kilani решил переехать. На прощание, Kilani решил дать Abd задачу, придуманную их общим соседом с таким же именем Abd.

Задача следующая:
Вам задано связное дерево с корнем в вершине $$$1$$$.
Вам нужно назначить каждой вершине букву a или b таким образом, чтобы суммарное количество a было равно $$$x$$$ и суммарное количество b было равно $$$n - x$$$.
Определим строку для каждой вершины $$$v$$$ дерева следующим образом:
- если $$$v$$$ — это корень, то строка — это одна буква, назначенная $$$v$$$:
- в противном случае, возьмем строку, полученную для родителя $$$p_v$$$ вершины $$$v$$$ и допишем к ней символ, назначенный $$$v$$$.
Расставьте буквы на вершинах таким образом, чтобы минимизировать количество различных строк среди строк для всех вершин.
В первой строке заданы два целых числа $$$n$$$ и $$$x$$$ ($$$1 \leq n \leq 10^5$$$; $$$0 \leq x \leq n$$$) — количество вершин в дереве и количество букв a.
Во второй строке заданы $$$n - 1$$$ целых чисел $$$p_2, p_3, \dots, p_{n}$$$ ($$$1 \leq p_i \leq n$$$; $$$p_i \neq i$$$), где $$$p_i$$$ — родитель вершины $$$i$$$.
Гарантируется, что входные данные описывают связное дерево.
В первой строке, выведите минимально возможное количество различных строк.
Во второй строке, выведите $$$n$$$ символов, каждый из которых — либо a, либо b и $$$i$$$-й символ — это символ, назначенный $$$i$$$-й вершине.
Удостоверьтесь, что букв a ровно $$$x$$$, а букв b ровно $$$n - x$$$.
Если существует несколько ответов, выведите любой из них.
9 3 1 2 2 4 4 4 3 1
4 aabbbbbba
Дерево из примера изображено ниже:
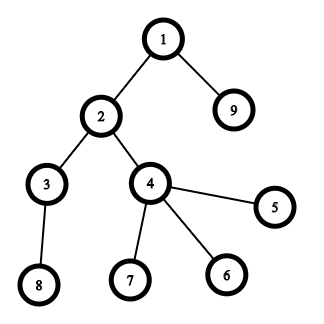
После назначения букв каждой вершине (в соответствии с выходными данными), дерево выглядит следующим образом:
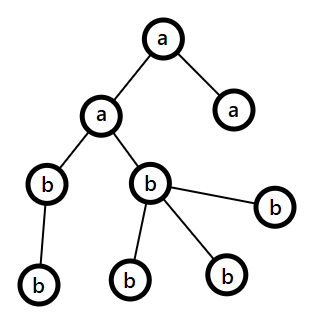
Строки для каждой вершины:
- строка вершины $$$1$$$: a
- строка вершины $$$2$$$: aa
- строка вершины $$$3$$$: aab
- строка вершины $$$4$$$: aab
- строка вершины $$$5$$$: aabb
- строка вершины $$$6$$$: aabb
- строка вершины $$$7$$$: aabb
- строка вершины $$$8$$$: aabb
- строка вершины $$$9$$$: aa
Множество различных строк равно $$$\{\text{a}, \text{aa}, \text{aab}, \text{aabb}\}$$$, то есть количество различных строк равно $$$4$$$.
| Название |
|---|




