| Codeforces Round 693 (Div. 3) |
|---|
| Закончено |
В Берляндии находятся $$$n$$$ городов. Город с номером $$$1$$$ является столицей. Некоторые пары городов соединены односторонней дорогой длины 1.
Перед поездкой Поликарп для каждого города узнал величину $$$d_i$$$ — расстояние от столицы (города с номером $$$1$$$) до города с номером $$$i$$$. Поликарп начинает своё путешествие в городе с номером $$$s$$$ и, находясь в $$$i$$$-м городе, выбирает одно из следующих действий:
- Поехать из $$$i$$$-го города в $$$j$$$-й, если существует дорога из $$$i$$$-го города в $$$j$$$-й и $$$d_i < d_j$$$;
- Поехать из $$$i$$$-го города в $$$j$$$-й, если существует дорога из $$$i$$$-го города в $$$j$$$-й и $$$d_i \geq d_j$$$;
- Прекратить путешествие.
Так как правительство Берляндии не хочет, чтобы все люди съезжались в столицу, поэтому Поликарп может не более одного раза совершить действие из пункта два. Иными словами, второе действие он может совершить $$$0$$$ или $$$1$$$ раз. Поликарп же, наоборот, хочет оказаться как можно ближе к столице.
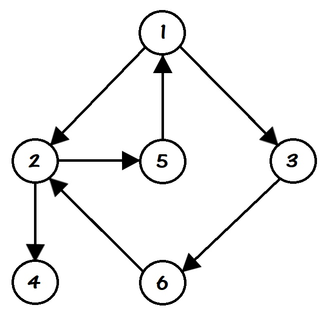
Например, если $$$n = 6$$$ и города соединены, как на картинке выше, то Поликарп мог совершить следующие путешествия (не все возможные варианты):
- $$$2 \rightarrow 5 \rightarrow 1 \rightarrow 2 \rightarrow 5$$$;
- $$$3 \rightarrow 6 \rightarrow 2$$$;
- $$$1 \rightarrow 3 \rightarrow 6 \rightarrow 2 \rightarrow 5$$$.
Поликарп хочет узнать для каждого стартового города $$$i$$$ узнать, на какое ближайшее расстояние он может подобраться к столице. Более формально: он хочет узнать минимальное значение $$$d_j$$$, такое что Поликарп может добраться из города $$$i$$$ в город $$$j$$$ по выше описанным правилам.
В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Далее следуют $$$t$$$ наборов входных данных.
Перед каждым набором входных данных расположена пустая строка.
Первая строка каждого набора содержит два целых числа $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) и $$$m$$$ ($$$1 \leq m \leq 2 \cdot 10^5$$$) — количество городов и дорог соответственно.
Далее следуют $$$m$$$ строк, описывающих дороги. Каждая дорога характеризуется двумя целыми числами $$$u$$$ и $$$v$$$ ($$$1 \leq u, v \leq n, u \ne v$$$) — номера городов, соединённых односторонней дорогой.
Гарантируется, что суммы $$$n$$$ и $$$m$$$ по всем наборам входных данных не превышают $$$2 \cdot 10^5$$$.
Гарантируется, что для каждой пары различных городов $$$(u, v)$$$ существует не более одной дороги из $$$u$$$ в $$$v$$$ (но пара встречных дорог из $$$u$$$ в $$$v$$$ и из $$$v$$$ в $$$u$$$ — допустима).
Гарантируется, что из столицы существует путь до всех городов.
Для каждого набора входных данных в отдельной строке выведите $$$n$$$ чисел, $$$i$$$-е из которых равно минимально возможному расстоянию от столицы до города, в котором Поликарп закончил своё путешествие.
3 6 7 1 2 1 3 2 5 2 4 5 1 3 6 6 2 2 2 1 2 2 1 6 8 1 2 1 5 2 6 6 1 2 3 3 4 4 2 5 4
0 0 1 2 0 1 0 0 0 0 2 1 1 0
| Название |
|---|




