Вы хотите построить забор, который будет состоять из $$$n$$$ равных секций. Все секции имеют ширину $$$1$$$ и высоту $$$k$$$. Вы поставите все секции в ряд бок о бок.
К сожалению, земля под забором далеко не плоская. Для простоты, вы можете считать что уровень земли под $$$i$$$-й секцией равен $$$h_i$$$.
Для постройки забора вам нужно следовать нескольким правилам:
- последовательные секции должны касаться сторонами и иметь ширину касания не менее $$$1$$$;
- первая и последняя секции должны стоять на своем уровне земли;
- секции между ними могут либо стоять на земле, либо находиться в воздухе, но не выше чем на $$$k - 1$$$ от уровня земли $$$h_i$$$ (высота над уровнем должна быть целым числом);
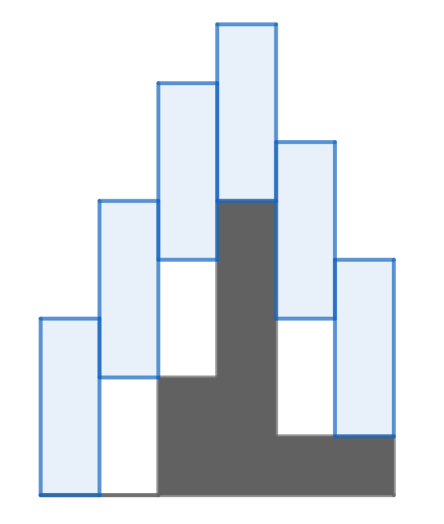 Один из возможных заборов (синего цвета) для первого набора входных данных
Один из возможных заборов (синего цвета) для первого набора входных данных Можно ли построить забор, удовлетворяющий всем правилам?
В первой строке задано единственное целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора заданы два целых числа $$$n$$$ и $$$k$$$ ($$$2 \le n \le 2 \cdot 10^5$$$; $$$2 \le k \le 10^8$$$) — количество секций в заборе и высота каждой секции.
Во второй строке каждого наборе заданы $$$n$$$ целых чисел $$$h_1, h_2, \dots, h_n$$$ ($$$0 \le h_i \le 10^8$$$), где $$$h_i$$$ — уровень земли под $$$i$$$-й секцией.
Гарантируется, что сумма $$$n$$$ по всем наборам не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных, выведите YES, если возможно построить забор, удовлетворяющий всем правилам. Иначе, выведите NO.
Вы можете выводить каждый символ в любом регистре (например, YES, Yes, yes, yEs будут определяться как положительный ответ).
3 6 3 0 0 2 5 1 1 2 3 0 2 3 2 3 0 2
YES YES NO
В первом наборе входных данных, один из возможных заборов изображен выше.
Во втором наборе, согласно второму правилу, вы должны построить обе секции на высоте земли, и, так как $$$k = 3$$$, $$$h_1 = 0$$$ и $$$h_2 = 2$$$, первое правило также выполняется.
В третьем наборе, согласно второму правилу, вы должны построить первую секцию на высоте $$$3$$$ и третью на высоте $$$2$$$. Согласно первому правилу, вторая секция должна быть на высоте не менее $$$2$$$ (чтобы иметь общую часть с первой секцией), но согласно третьему правилу, вторая секция должна быть на высоте не более $$$h_2 + k - 1 = 1$$$.
| Название |
|---|




