| Codeforces Round 688 (Div. 2) |
|---|
| Закончено |
Gildong играет в игру со своей собакой, Badugi. Они находятся в парке, в котором есть $$$n$$$ перекрестков и $$$n-1$$$ двусторонних дорог, длиной в $$$1$$$ и соединяющих два перекрестка. Пересечения пронумерованы от $$$1$$$ до $$$n$$$, и для каждой пары $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le n$$$), возможно пройти от $$$b$$$-го перекрестка до $$$a$$$-го передвигаясь по дорогам.
Gildong поставил одну закуску на каждый перекресток. Gildong поставил Badugi задачу — съесть все закуски. Badugi начинает на $$$1$$$-м перекрестке, и он передвигается по следующим правилам:
- Badugi ищет закуски, которые находятся к нему как можно ближе. Расстояние это длина кратчайшего пути от текущей позиции Badugi до перекрестка с закуской. Однако, обоняние Badugi ограничено до $$$k$$$ метров, так что он может находить только закуски на расстоянии не больше чем $$$k$$$ метров от текущей позиции. Если он не может найти ни одной закуски, задание считается проваленным.
- Среди всех закусок, которые Badugi чувствует на его текущей позиции, он выбирает закуску с минимальным расстоянием до текущей позиции. Если есть несколько возможных закусок, он выбирает одну любую из них.
- Он повторяет этот процесс пока он не съест все $$$n$$$ закусок. После этого, он должен снова найти $$$1$$$-й перекресток, который должен быть на расстоянии не больше чем $$$k$$$ метров от последней съеденной закуски. Если он может найти его, он проходит задание. Иначе, задание считается проваленным.
К сожалению, Gildong не знает значение $$$k$$$. Таким образом, он просит вас найти минимальное значение $$$k$$$, при котором Badugi сможет выполнить задание, если будет действовать оптимально.
Тест состоит из одного или нескольких наборов входных данных. В первой строке записано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10^4$$$).
В первой строке каждого набора входных данных записано одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество перекрестков в парке.
В каждой из следующих $$$n-1$$$ строк записаны два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$, $$$u \ne v$$$) , которые описывают двунаправленную дорогу между перекрестками $$$u$$$ и $$$v$$$. Все дороги двухсторонние и различны.
Гарантируется, что:
- Для каждого набора входных данных, для каждой пары $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le n$$$), возможно пройти от $$$b$$$-го перекрестка до $$$a$$$-го передвигаясь по дорогам.
- Сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — минимальное возможное значение $$$k$$$, при котором Badugi может выполнить свое задание.
3 3 1 2 1 3 4 1 2 2 3 3 4 8 1 2 2 3 3 4 1 5 5 6 6 7 5 8
2 3 3
В первом наборе входных данных, Badugi может выполнить задание для $$$k=2$$$, передвигаясь следующим образом:
- Исходно, Badugi находится на $$$1$$$-м перекрестке. Ближайшая закуска, очевидно, находится на $$$1$$$-м перекрестке, поэтому он съедает ее.
- Затем, он ищет ближайшую закуску, которая может быть либо на $$$2$$$-м или на $$$3$$$-м перекрестке. Предположим, что он выбирает $$$2$$$-й перекресток. Он переходит на $$$2$$$-й перекресток, который находится на расстоянии $$$1$$$ метр, и ест закуску.
- Единственная закуска находится на $$$3$$$-м перекрестке, и ему нужно пройти по $$$2$$$ дорогам, чтобы дойти до нее.
- После съедения закуски на $$$3$$$-м перекрестке, ему снова нужно найти $$$1$$$-й перекресток, который находится на расстоянии $$$1$$$ метр. После того как он возвращается на него, он выполнил свое задание.
Во втором наборе входных данных, единственная возможная последовательность действий это $$$1$$$ – $$$2$$$ – $$$3$$$ – $$$4$$$ – $$$1$$$. Так как расстояние между $$$4$$$-м и $$$1$$$-м перекрестком равно $$$3$$$, $$$k$$$ должно быть хотя бы $$$3$$$ для того, чтобы Badugi смог выполнить задание.
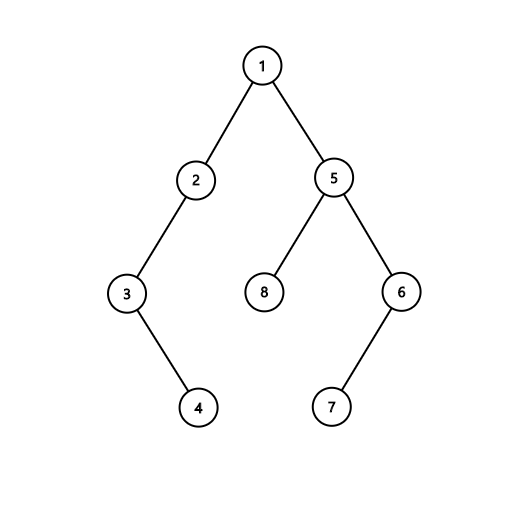
В третьем наборе входных данных, Badugi может двигаться следующим образом: $$$1$$$ – $$$5$$$ – $$$6$$$ – $$$7$$$ – $$$8$$$ – $$$2$$$ – $$$3$$$ – $$$4$$$ – $$$1$$$. Можно показать, что это единственный вариант для Badugi выполнить миссию с $$$k=3$$$.
| Название |
|---|




