| Codeforces Global Round 12 |
|---|
| Закончено |
У вас есть $$$n$$$ различных точек $$$(x_1, y_1),\ldots,(x_n,y_n)$$$ на плоскости и неотрицательное целое число $$$k$$$. Каждая точка представляет собой микроскопический стальной шарик, а $$$k$$$ — это его сила притяжения, когда он заряжен. Сила притяжения одинакова для всех шариков.
За одну операцию вы можете выбрать шарик $$$i$$$ и зарядить его. После этого все шарики на манхеттенском расстоянии не более $$$k$$$ от шарика $$$i$$$ перемещаются в позицию шарика $$$i$$$. После этой операции несколько различных шариков могут оказаться в одной точке.
Более формально, для всех шариков $$$j$$$ таких, что $$$|x_i - x_j| + |y_i - y_j| \le k$$$, мы присваиваем $$$x_j:=x_i$$$ и $$$y_j:=y_i$$$.
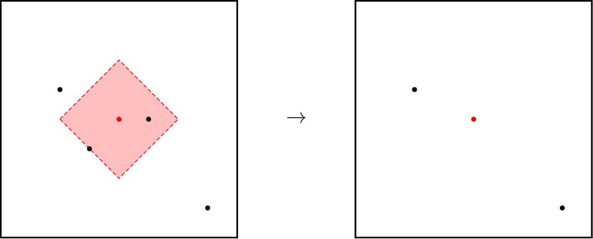 Пример операции. После зарядки шарика в центре два других шарика перемещаются в его позицию. На правой картинке красная точка в центре — это общее положение этих шариков после операции.
Пример операции. После зарядки шарика в центре два других шарика перемещаются в его позицию. На правой картинке красная точка в центре — это общее положение этих шариков после операции. Ваша задача — найти минимальное количество операций, нужное для того, чтобы переместить все шарики в одну точку, или сообщить, что это сделать невозможно.
В первой строке находится единственное целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных.
В первой строке описания каждого набора входных данных находится два целых числа $$$n$$$, $$$k$$$ ($$$2 \le n \le 100$$$, $$$0 \le k \le 10^6$$$) — количество шариков и сила притяжения каждого шарика, соответственно.
Следующие $$$n$$$ строк описывают координаты шариков. В $$$i$$$-й из этих строк находится два целых числа $$$x_i$$$, $$$y_i$$$ ($$$0 \le x_i, y_i \le 10^5$$$) — координаты $$$i$$$-о шарика.
Гарантируется, что все точки различны.
Для каждого набора входных данных выведите единственное целое число — минимальное количество операций, нужное для того, чтобы переместить все шарики в одну точку, или $$$-1$$$, если это сделать невозможно.
3 3 2 0 0 3 3 1 1 3 3 6 7 8 8 6 9 4 1 0 0 0 1 0 2 0 3
-1 1 -1
В первом наборе входных данных три шарика находятся в $$$(0, 0)$$$, $$$(3, 3)$$$, и $$$(1, 1)$$$ и сила притяжения равна $$$2$$$. Можно переместить два шарика в одну точку за одну операцию, но невозможно переместить все три шарика в одну точку за любое количество операций.
Во втором наборе входных данных три шарика находятся шарика в $$$(6, 7)$$$, $$$(8, 8)$$$, и $$$(6, 9)$$$ и сила притяжения равна $$$3$$$. Если мы зарядим любой шарик, другие два переместятся в его позицию, поэтому нам достаточно одной операции.
В третьем наборе входных данных четыре шарика находятся в $$$(0, 0)$$$, $$$(0, 1)$$$, $$$(0, 2)$$$ и $$$(0, 3)$$$ и сила притяжения равна $$$1$$$. Можно показать, что невозможно переместить все шарики в одну и ту же точку какой-то последовательностью операций.
| Название |
|---|




