Начался новый учебный год, и в университет Берляндии пришли $$$n$$$ новых студентов, которых разбили на $$$k$$$ групп, причем некоторые группы могли оказаться пустыми. Среди студентов есть $$$m$$$ пар знакомых, причём знакомые студенты могут быть как из одной, так и из разных групп.
Алиcа, как куратор нового набора, позвала всех новоприбывших на организационную встречу. На ней она хочет устроить игру, чтобы еще незнакомые студенты получше узнали друг друга. Для этого она выберет две группы, студенты из которых будут играть. При этом правила игры требуют разделить участников на две команды так, чтобы внутри каждой из команд никто не знал друг друга.
Алиcу интересует: сколько существует способов выбрать две различные группы студентов так, чтобы получилось сыграть в игру по всем правилам. При этом в игре должны участвовать все студенты обеих групп.
Обратите внимание, что команды, на которые Алиca разделит студентов, не обязаны совпадать с группами, в которых учатся участники. Более того, команды могут быть разного размера (или даже пустыми).
В первой строке заданы три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$1 \le n \le 500\,000$$$; $$$0 \le m \le 500\,000$$$; $$$2 \le k \le 500\,000$$$) — количество студентов, количество пар знакомых студентов и количество групп, соответственно.
Во второй строке заданы $$$n$$$ целых чисел $$$c_1, c_2, \dots, c_n$$$ ($$$1 \le c_i \le k$$$), где $$$c_i$$$ равняется номеру группы, в которой учится $$$i$$$-й студент.
Далее следуют $$$m$$$ строк. В $$$i$$$-й строке заданы два числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$), означающие, что $$$a_i$$$-й и $$$b_i$$$-й студент знают друг друга. Гарантируется, что $$$a_i \neq b_i$$$, и что если пара студентов знает друг друга, то она встречается ровно один раз.
Выведите одно число — количество способов выбрать две различные группы так, чтобы получилось сыграть в игру по всем правилам.
6 8 3 1 1 2 2 3 3 1 3 1 5 1 6 2 5 2 6 3 4 3 5 5 6
2
4 3 3 1 1 2 2 1 2 2 3 3 4
3
4 4 2 1 1 1 2 1 2 2 3 3 1 1 4
0
5 5 2 1 2 1 2 1 1 2 2 3 3 4 4 5 5 1
0
Граф знакомств для первого тестового примера выглядит следующим образом (рядом с каждым студентом подписан номер его группы):
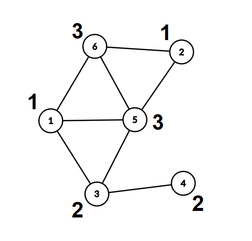
В данном случае нам подходят способы:
- Выбрать первую и вторую группу — например, можно отнести студентов номер $$$1$$$ и $$$4$$$ к первой команде, а студентов номер $$$2$$$ и $$$3$$$ ко второй.
- Выбрать вторую и третью группу — можно отнести студентов номер $$$3$$$ и $$$6$$$ к первой команде, а студентов номер $$$4$$$ и $$$5$$$ ко второй.
- Выбрать первую и третью группы мы не можем, потому что не существует разбиения на команды, удовлетворяющего правилам игры.
Во втором тестовом примере мы можем выбрать любую пару групп. Обратите внимание, что несмотря на то, что в третьей группе нет студентов, мы все равно можем ее выбирать.
| Название |
|---|




