У Монокарпа было дерево из $$$n$$$ вершин с корнем в вершине $$$1$$$. Он решил изучить алгоритм BFS (Поиск в ширину), и поэтому запустил BFS на своем дереве, стартуя с корня. Упрощенно, BFS можно описать следующим псевдокодом:
a = [] # порядок, в котором вершины обработались
q = Queue()
q.put(1) # кладем корень в конец очереди
while not q.empty():
k = q.pop() # достаем вершину из начала очереди
a.append(k) # кладем k в конец последовательности, описывающей порядок посещения вершин
for y in g[k]: # g[k] — это список всех детей вершины k, отсортированный в порядке возрастания
q.put(y)
Монокарп был так восхищен алгоритмом BFS, что в результате потерял свое дерево. К счастью, у него осталась последовательность вершин в порядке их посещения алгоритмом BFS (массив a из псевдокода). Монокарп знает, что каждая вершина была посещена ровно один раз (так как они кладутся и забираются из очереди ровно один раз). Также он знает, что все дети каждой вершины были просмотрены в порядке возрастания.
Монокарп понимает, что есть много деревьев (в общем случае) с одинаковым порядком посещения $$$a$$$, поэтому даже не надеется восстановить свое дерево. Монокарпа устроит любое дерево минимально возможной высоты.
Высота дерева — это максимум среди глубин вершин дерева, и глубина вершины — это количество дуг на пути от корня до этой вершины. Например, глубина вершины $$$1$$$ равна $$$0$$$, так как она является корнем, а глубина любого из детей корня равна $$$1$$$.
Помогите Монокарпу найти любое дерево с заданным порядком посещения $$$a$$$ и минимальной высотой.
В первой строке задано единственное целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных.
В первой строке каждого набора задано одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Во второй строке каждого набора заданы $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le n$$$; $$$a_i \neq a_j$$$; $$$a_1 = 1$$$) — порядок посещения вершин алгоритмом BFS.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных, выведите минимально возможную высоту дерева с заданным порядком обхода $$$a$$$.
3 4 1 4 3 2 2 1 2 3 1 2 3
3 1 1
В первом наборе входных данных, есть только одно дерево с заданным порядком посещения:
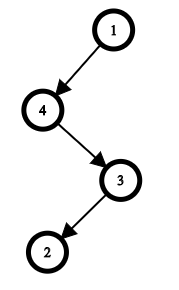
Во втором наборе, также есть только одно дерево с заданным порядком посещения:
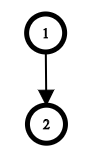
В третьем наборе, оптимальное дерево с заданным порядком посещения изображено ниже:
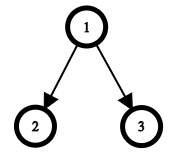
| Название |
|---|




