Это интерактивная задача.
Чтобы помешать озорным кроликам свободно бродить по зоопарку, смотритель зоопарка установил специальный замок для кроличьего вольера. Этот замок называется поворотным лазерным замком.
Замок состоит из $$$n$$$ концентрических колец, пронумерованных от $$$0$$$ до $$$n-1$$$. Внутреннее кольцо имеет номер $$$0$$$, а самое дальнее кольцо имеет номер $$$n-1$$$. Все кольца разделены на $$$nm$$$ одинаковых секций каждая. Каждое из этих колец содержит одну металлическую дугу, которая покрывает ровно $$$m$$$ последовательных секций. В центре кольца находится ядро, а вокруг всего замка расположено $$$nm$$$ сенсоров, выровненных по границам $$$nm$$$ секций.
Ядро содержит $$$nm$$$ лазеров, которые светят из центра, по одному внутри каждой секции. Лазеры могут быть заблокированы одной из дуг. У замка есть дисплей, который показывает количество сенсоров, в которые попал лазер.
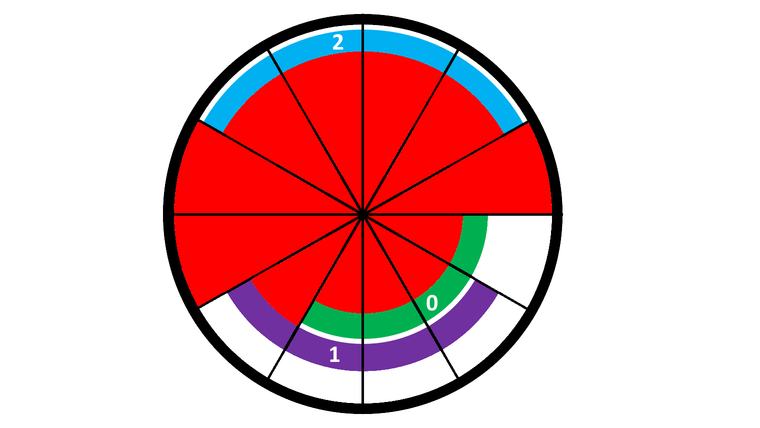
В приведенном примере есть $$$n=3$$$ кольца, каждое покрывает $$$m=4$$$ секции. Дуги покрашены в зеленый (в кольце $$$0$$$), фиолетовый (в кольце $$$1$$$) и голубой (в кольце $$$2$$$). Лучи лазеров изображены красным. Всего есть $$$nm=12$$$ секций, и $$$3$$$ лазера не заблокированы ни одной дугой, поэтому дисплей будет показывать число $$$3$$$ в этом случае.
Кролик пытается открыть замок, чтобы освободить всех кроликов, но замок абсолютно непрозрачен, поэтому он не видит положений дуг замка. Имея относительные позиции дуг, кролик сможет открыть замок сам.
Формально, кролику нужна последовательность из $$$n-1$$$ целого числа $$$p_1,p_2,\ldots,p_{n-1}$$$, удовлетворяющая $$$0 \leq p_i < nm$$$ такая, что для всех $$$i$$$ $$$(1 \leq i < n)$$$ кролик может повернуть кольцо $$$0$$$ по часовой стрелке ровно $$$p_i$$$ раз так, что множество секций, которое будет покрывать кольцо $$$0$$$, совпадает с множеством секций, которое будет покрывать кольцо $$$i$$$. В приведенном выше примере относительные позиции $$$p_1 = 1$$$ и $$$p_2 = 7$$$.
Чтобы открыть замок он может взять одно из $$$n$$$ колец и повернуть его на $$$1$$$ секцию либо по часовой стрелке, либо против часовой стрелки. После каждого поворота вы будете видеть число, изображенное на дисплее.
Поскольку у него маленькие лапки, кролик попросил вас помочь ему найти относительные позиции дуг после всех поворотов, которые вы сделаете. Вы можете сделать не больше $$$15000$$$ поворотов перед тем, как у кролика кончится терпение.
В первой строке находятся два целых числа $$$n$$$ и $$$m$$$ $$$(2 \leq n \leq 100, 2 \leq m \leq 20)$$$: количество колец и количество секций, которое покрывает каждая дуга.
Чтобы сделать поворот, выведите в единственной строке «? x d», где $$$x$$$ $$$(0 \leq x < n)$$$ это номер кольца, которое вы хотите повернуть, а $$$d$$$ $$$(d \in \{-1,1\})$$$ — это направление, в котором вы хотите его повернуть. $$$d=1$$$ обозначает поворот на $$$1$$$ секцию по часовой стрелке, $$$d=-1$$$ обозначает поворот на $$$1$$$ секцию против часовой стрелки.
Для каждого запроса в ответ вы получите единственное целое число $$$a$$$: количество лазеров, которые не заблокированы ни одной из дуг после поворота, который был сделан.
Когда вы определили относительные позиции дуг, выведите «!» и затем $$$n-1$$$ целое число $$$p_1, p_2, \ldots, p_{n-1}$$$.
Обратите внимание, что позиции дуг зафиксированы заранее для каждого теста и не будут меняться в процессе взаимодействия.
После вывода запроса не забывайте сделать перевод строки и очистить буфер выходного потока. Иначе ваша программа получит вердикт Idleness limit exceeded.
Чтобы это сделать, используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- Обратитесь к документации для других языков.
Взломы:
Чтобы сделать взлом, используйте следующий формат:
В первой строке находятся два целых числа $$$n$$$ и $$$m$$$.
Следующая строка должна содержать $$$n-1$$$ целое число $$$p_1,p_2,\ldots,p_{n-1}$$$: относительные позиции колец $$$1,2,\ldots,n-1$$$.
3 4 4 4 3
? 0 1 ? 2 -1 ? 1 1 ! 1 5
Первый тест соответствует картинке из условия задачи.
После первого поворота (который заключается в повороте кольца $$$0$$$ по часовой стрелке на $$$1$$$ секцию) мы получим следующую конфигурацию:
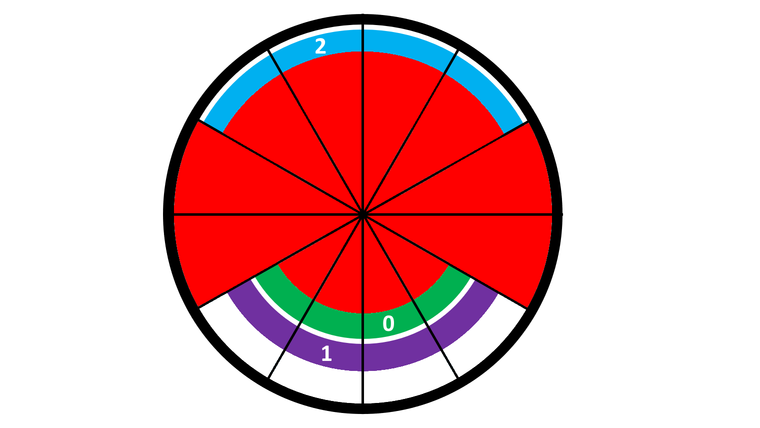
После второго поворота (который заключается в повороте кольца $$$2$$$ против часовой стрелки на $$$1$$$ секцию) мы получим следующую конфигурацию:
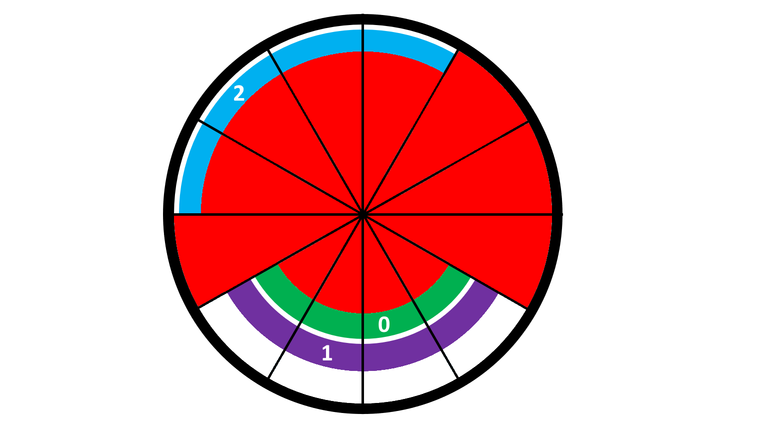
После третьего поворота (который заключается в повороте кольца $$$1$$$ по часовой стрелке на $$$1$$$ секцию) мы получим следующую конфигурацию:
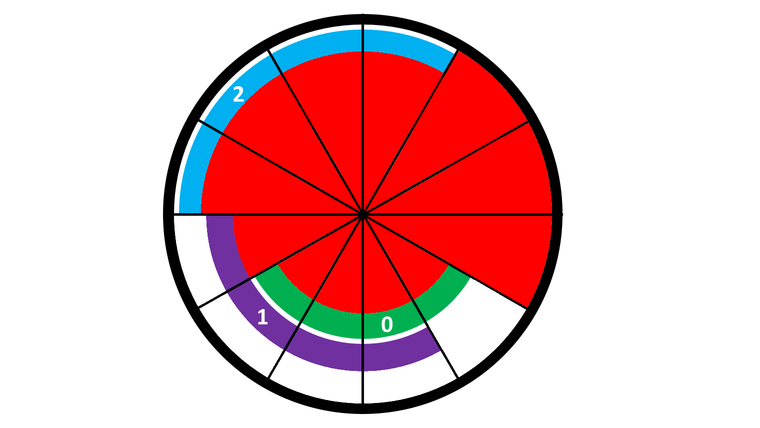
Если мы повернем кольцо $$$0$$$ по часовой стрелке один раз, мы увидим, что множество секций, которое покрывает кольцо $$$0$$$, совпадает с множеством секций, которое покрывает кольцо $$$1$$$, поэтому $$$p_1=1$$$.
Если мы повернем кольцо $$$0$$$ по часовой стрелке пять раз, мы увидим, что множество секций, которое покрывает кольцо $$$0$$$, совпадает с множеством секций, которое покрывает кольцо $$$2$$$, поэтому $$$p_2=5$$$.
Обратите внимание, что если бы мы сделали другой набор поворотов, ответом могли бы быть другие значения $$$p_1$$$ и $$$p_2$$$.
| Название |
|---|




