| Codeforces Round 676 (Div. 2) |
|---|
| Закончено |
Линдси Букингем сказала Стиви Никс «идти своим путем». Никс сейчас грустит и хочет уйти как можно быстрее, но она живет в двухмерном шестиугольном мире.
Рассмотрим шестиугольное покрытие плоскости, как на картинке ниже.

Ники хочет добраться от ячейки с координатами $$$(0, 0)$$$ к определенной ячейке, заданной координатами. Она может перейти от шестиугольника к любому из шести своих соседей, но у каждого из переходов есть своя стоимость. Стоимость зависит от направления, в котором вы путешествуете. Таким образом, переход от $$$(0, 0)$$$ до $$$(1, 1)$$$ будет стоить ровно столько же, как и переход от $$$(-2, -1)$$$ до $$$(-1, 0)$$$. Стоимости приведены во входных данных в порядке $$$c_1$$$, $$$c_2$$$, $$$c_3$$$, $$$c_4$$$, $$$c_5$$$, $$$c_6$$$, как на рисунке ниже.
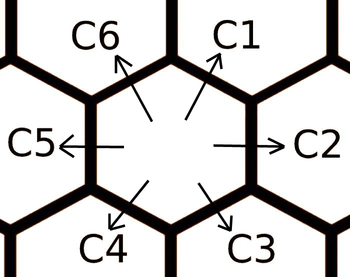
Выведите наименьшую стоимость пути от начала координат, который имеет координаты $$$(0, 0)$$$, к данной ячейке.
Каждый тест содержит несколько наборов входных данных. В первой строке указано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10^{4}$$$). Описание наборов входных данных приведено ниже.
Первая строка каждого набора входных данных содержит два целых числа $$$x$$$ и $$$y$$$ ($$$-10^{9} \le x, y \le 10^{9}$$$) — координаты конечного шестиугольника.
Вторая строка каждого набора входных данных содержит шесть целых чисел $$$c_1$$$, $$$c_2$$$, $$$c_3$$$, $$$c_4$$$, $$$c_5$$$, $$$c_6$$$ ($$$1 \le c_1, c_2, c_3, c_4, c_5, c_6 \le 10^{9}$$$) — стоимости совершения одного шага в определенном направлении (см. рисунок выше).
Для каждого набора входных данных выведите наименьшую стоимость пути от начала координат до данной клетки.
2 -3 1 1 3 5 7 9 11 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
18 1000000000000000000
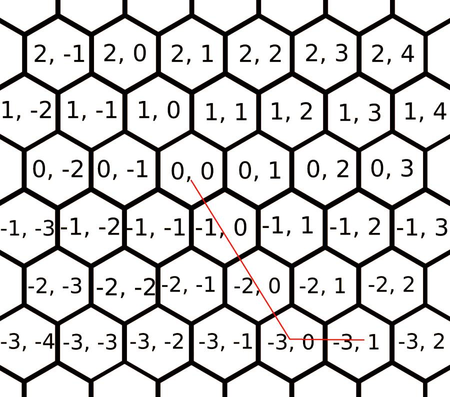
На рисунке ниже показано решение для первого примера. Стоимость $$$18$$$ достигается путем трехкратного взятия $$$c_3$$$ и $$$c_2$$$ один раз, что составляет $$$5+5+5+3=18$$$.
| Название |
|---|




