| Codeforces Round 670 (Div. 2) |
|---|
| Закончено |
Fishing Prince любит деревья и особенно он любит деревья с ровно одним центроидом. Деревом называется связный граф без циклов.
Вершина называется центроидом дерева тогда и только тогда, когда при удалении этой вершины (удалении вершины и всех выходящих из нее ребер) размер наибольшей компоненты связности оставшегося графа будет наименьший возможный.
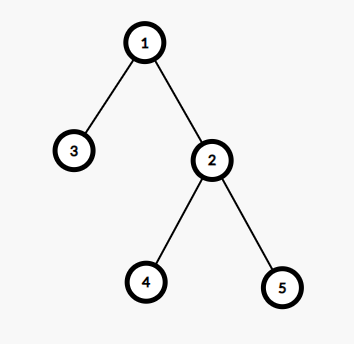
Например, вершина $$$2$$$ является центроидом дерева на следующей картинке, потому что после того, как вы удалите ее, размер наибольшей компоненты связности оставшегося графа будет равен $$$2$$$. Невозможно удалить другую вершину, чтобы этот размер был меньше.
Однако, в некоторых деревьях может быть больше одного центроида, например:
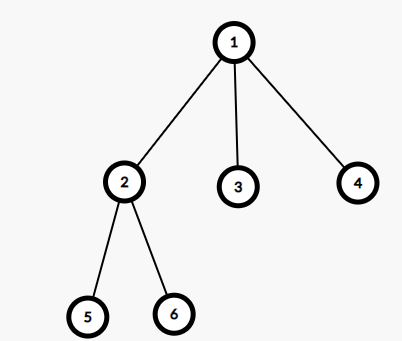
Обе вершины $$$1$$$ и $$$2$$$ являются центроидами, потому что размер наибольшей компоненты связности будет равен $$$3$$$ после удаления любой из них.
Сейчас у Fishing Prince есть дерево. Он должен удалить одно ребро дерева. После этого он должен добавить одно ребро. Получившийся после этих двух операций граф снова должен стать деревом. Можно добавить только что удаленное ребро.
Он хочет, чтобы у получившегося дерева был единственный центроид. Помогите ему и найдите любую возможную пару операций, которые можно сделать. Можно доказать, что хотя бы один способ сделать такую пару операций существует.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится единственное целое число $$$t$$$ ($$$1\leq t\leq 10^4$$$) — количество наборов входных данных. Описание наборов входных данных следует.
В первой строке описания каждого набора входных данных находится целое число $$$n$$$ ($$$3\leq n\leq 10^5$$$) — количество вершин.
Каждая из следующей $$$n-1$$$ строки содержит два целых числа $$$x, y$$$ ($$$1\leq x,y\leq n$$$). Они означают, что существует ребро, соединяющее вершины $$$x$$$ и $$$y$$$.
Гарантируется, что данный граф является деревом.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите две строки.
В первой строке выведите два целых числа $$$x_1, y_1$$$ ($$$1 \leq x_1, y_1 \leq n$$$), которые означают, что вы удаляете ребро между вершинами $$$x_1$$$ и $$$y_1$$$. Должно существовать ребро, соединяющее вершины $$$x_1$$$ и $$$y_1$$$.
Во второй строке выведите два целых числа $$$x_2, y_2$$$ ($$$1 \leq x_2, y_2 \leq n$$$), которые означают, что вы добавляете ребро между вершинами $$$x_2$$$ и $$$y_2$$$.
Граф, получающийся после применения этих двух операций, должен снова являться деревом.
Если существует несколько возможных решений, выведите любое.
2 5 1 2 1 3 2 4 2 5 6 1 2 1 3 1 4 2 5 2 6
1 2 1 2 1 3 2 3
Обратите внимание, что вы можете добавлять то же самое ребро, которое вы удалили.
В первом наборе входных данных после удаления и добавления одного и того же ребра вершина $$$2$$$ по-прежнему останется единственным центроидом.
Во втором наборе входных данных вершина $$$2$$$ станет единственным центроидом после удаления ребра между вершинами $$$1$$$ и $$$3$$$ и добавления ребра между вершинами $$$2$$$ и $$$3$$$.
| Название |
|---|




