| Codeforces Round 668 (Div. 1) |
|---|
| Закончено |
Алиса и Боб играют в забавную игру — догонялки на дереве.
В эту игру играют на дереве из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$. Напомним, что дерево на $$$n$$$ вершинах — это неориентированный, связный граф с $$$n-1$$$ ребрами.
Изначально Алиса располагается в вершине $$$a$$$, а Боб — в вершине $$$b$$$. Они ходят по очереди, и Алиса делает первый ход. За свой ход Алиса может перепрыгнуть в вершину с расстоянием не более $$$da$$$ от текущей вершины. Боб же за свой ход может перепрыгнуть в вершину с расстоянием не более $$$db$$$ от текущей вершины. Расстояние между двумя вершинами определяется как количество рёбер на уникальном простом пути между ними. В частности, любому из игроков разрешается остаться на одной и той же вершине в свой ход. Заметим, что при выполнении хода игрок занимает только начальную и конечную вершины своего хода, а не вершины между ними.
Если после не более чем $$$10^{100}$$$ ходов Алиса и Боб занимают одну и ту же вершину, то победителем объявляется Алиса. В противном случае побеждает Боб.
Определите победителя, если оба игрока играют оптимально.
Каждый тест содержит несколько наборов входных данных. В первой строке указано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10^4$$$). Описание наборов входных данных приведено ниже.
Первая строка каждого набора входных данных содержит пять целых чисел $$$n,a,b,da,db$$$ ($$$2\le n\le 10^5$$$, $$$1\le a,b\le n$$$, $$$a\ne b$$$, $$$1\le da,db\le n-1$$$) — количество вершин, вершину Алисы, вершину Боба, максимальное расстояние прыжка Алисы и максимальное расстояние прыжка Боба, соответственно.
Следующие $$$n-1$$$ строк описывают ребра дерева. $$$i$$$-я из этих строк содержит два целых числа $$$u$$$, $$$v$$$ ($$$1\le u, v\le n, u\ne v$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что данный граф является деревом.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$10^5$$$.
Для каждого набора входных данных выведите одну строку, содержащую победителя игры: «Alice» или «Bob».
4 4 3 2 1 2 1 2 1 3 1 4 6 6 1 2 5 1 2 6 5 2 3 3 4 4 5 9 3 9 2 5 1 2 1 6 1 9 1 3 9 5 7 9 4 8 4 3 11 8 11 3 3 1 2 11 9 4 9 6 5 2 10 3 2 5 9 8 3 7 4 7 10
Alice Bob Alice Alice
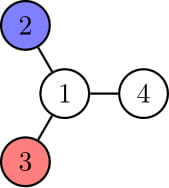
В первом наборе входных данных Алиса может выиграть, перейдя к вершине $$$1$$$. Тогда куда бы Боб не двигался дальше, Алиса сможет перейти к той же самой вершине на следующем шаге.
Во втором наборе входных данных у Боба есть следующая победная стратегия. Куда бы Алиса ни двигалась, Боб всегда будет двигаться к той из вершин $$$1$$$ или $$$6$$$, которая более удалена от Алисы.

| Название |
|---|




