| Codeforces Round 665 (Div. 2) |
|---|
| Закончено |
У вас есть квадрат размера $$$10^6 \times 10^6$$$ на координатной плоскости с вершинами в точках $$$(0, 0)$$$, $$$(0, 10^6)$$$, $$$(10^6, 0)$$$ и $$$(10^6, 10^6)$$$.
Вы собираетесь нарисовать несколько отрезков на плоскости. Все отрезки либо горизонтальные, либо вертикальные и пересекаются хотя бы с одной стороной квадрата.
Сейчас вас интересует: на какое количество частей разобьется данный квадрат после того, как будут нарисованы все отрезки. Напишите программу, подсчитывающую количество частей.
В первой строке заданы два целых числа $$$n$$$ и $$$m$$$ ($$$0 \le n, m \le 10^5$$$) — количество горизонтальных и вертикальных отрезков, соответственно.
В следующих $$$n$$$ строках заданы описания горизонтальных отрезков. В $$$i$$$-й строке заданы три целых числа $$$y_i$$$, $$$lx_i$$$ и $$$rx_i$$$ ($$$0 < y_i < 10^6$$$; $$$0 \le lx_i < rx_i \le 10^6$$$), означающих отрезок, соединяющий $$$(lx_i, y_i)$$$ и $$$(rx_i, y_i)$$$.
В следующих $$$m$$$ строках заданы описания вертикальных отрезков. В $$$i$$$-й строке заданы три целых числа $$$x_i$$$, $$$ly_i$$$ и $$$ry_i$$$ ($$$0 < x_i < 10^6$$$; $$$0 \le ly_i < ry_i \le 10^6$$$), означающих отрезок, соединяющий $$$(x_i, ly_i)$$$ и $$$(x_i, ry_i)$$$.
Гарантируется, что никакие два отрезка не лежат на одной прямой и каждый отрезок пересекается хотя бы с одной стороной квадрата.
Выведите количество частей, на которые разбивается квадрат после того, как нарисованы все отрезки.
3 3 2 3 1000000 4 0 4 3 0 1000000 4 0 1 2 0 5 3 1 1000000
7
Пример выглядит следующим образом:
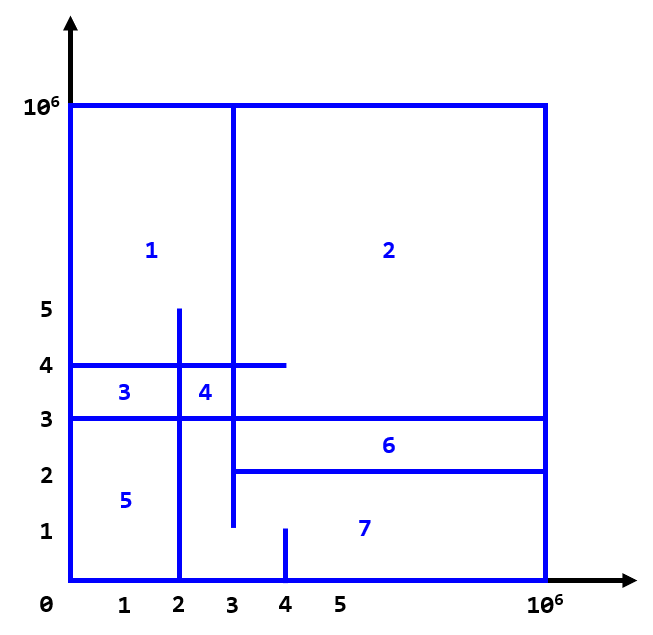
| Название |
|---|




