| Codeforces Round 665 (Div. 2) |
|---|
| Закончено |
Вам задано дерево, состоящее из $$$n$$$ вершин. Вы должны сопоставить каждому из $$$n-1$$$ ребер этого дерева целое число таким образом, чтобы выполнялись следующие условия:
- каждое число должно быть целым и строго больше $$$0$$$;
- произведение всех $$$n-1$$$ чисел должно быть равно $$$k$$$;
- количество $$$1$$$-ц среди всех $$$n-1$$$ чисел должно быть минимально возможным.
Назовем $$$f(u,v)$$$ сумму чисел на простом пути из вершины $$$u$$$ в вершину $$$v$$$. Также, назовем $$$\sum\limits_{i=1}^{n-1} \sum\limits_{j=i+1}^n f(i,j)$$$ как индекс распределения дерева.
Определите максимально возможный индекс распределения, который можно получить. Так как ответ может быть слишком большим, выведите его по модулю $$$10^9 + 7$$$.
В данной задаче, так как число $$$k$$$ может быть слишком большим, задана факторизация $$$k$$$ на простые числа.
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных.
В первой строке каждого набора задано одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество вершин в дереве.
В каждой из следующих $$$n-1$$$ строк заданы ребра: в $$$i$$$-й строке заданы два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \ne v_i$$$) — номера вершин, соединенных $$$i$$$-м ребром.
В следующей строке задано одно число $$$m$$$ ($$$1 \le m \le 6 \cdot 10^4$$$) — количество простых в факторизации $$$k$$$.
В следующей строке заданы $$$m$$$ простых чисел $$$p_1, p_2, \ldots, p_m$$$ ($$$2 \le p_i < 6 \cdot 10^4$$$) такие, что $$$k = p_1 \cdot p_2 \cdot \ldots \cdot p_m$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$, сумма $$$m$$$ по всем наборам не превосходит $$$6 \cdot 10^4$$$, и что заданные ребра в каждом наборе образуют дерево.
Выведите максимально возможный индекс распределения. Так как ответ может быть слишком большим, выведите его по модулю $$$10^9+7$$$.
3 4 1 2 2 3 3 4 2 2 2 4 3 4 1 3 3 2 2 3 2 7 6 1 2 3 4 6 7 3 5 1 3 6 4 7 5 13 3
17 18 286
В первом наборе входных данных, один из возможных ответов изображен на рисунке ниже:

В данном случае, $$$f(1,2)=1$$$, $$$f(1,3)=3$$$, $$$f(1,4)=5$$$, $$$f(2,3)=2$$$, $$$f(2,4)=4$$$, $$$f(3,4)=2$$$, и сумма этих $$$6$$$ чисел равна $$$17$$$.
Во втором наборе входных данных, один из возможных ответов изображен ниже:
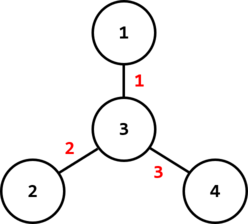
В этом случае, $$$f(1,2)=3$$$, $$$f(1,3)=1$$$, $$$f(1,4)=4$$$, $$$f(2,3)=2$$$, $$$f(2,4)=5$$$, $$$f(3,4)=3$$$, и сумма этих $$$6$$$ чисел равна $$$18$$$.
| Название |
|---|




