Скоро начинаются соревнования по бегу. Стадион, на котором планируется их проводить, может быть представлен несколькими отрезками на координатной плоскости:
- два горизонтальных отрезка: один соединяет точки $$$(0, 0)$$$ и $$$(x, 0)$$$, другой соединяет точки $$$(0, y)$$$ и $$$(x, y)$$$;
- $$$n + 1$$$ вертикальный отрезок, пронумерованные от $$$0$$$ до $$$n$$$. $$$i$$$-й отрезок соединяет точки $$$(a_i, 0)$$$ и $$$(a_i, y)$$$; $$$0 = a_0 < a_1 < a_2 < \dots < a_{n - 1} < a_n = x$$$.
Например, на данной картинке изображен стадион с $$$x = 10$$$, $$$y = 5$$$, $$$n = 3$$$ и $$$a = [0, 3, 5, 10]$$$:
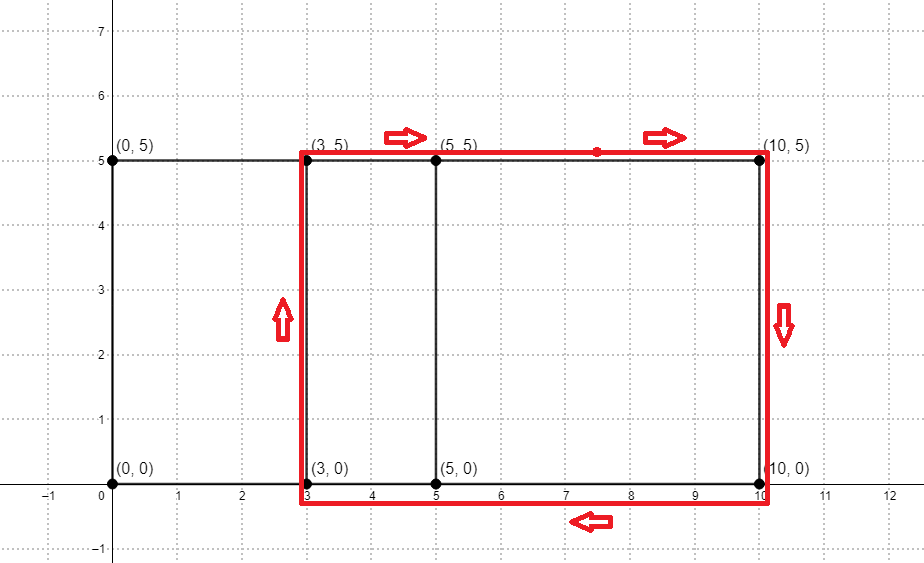
Назовем кругом такой маршрут, который проходит по отрезкам, начинается и заканчивается в одно точке и никогда не пересекается сам с собой (единственные две совпадающие точки круга — это стартовая и финишная). Длина круга — это суммарное расстояние, пройденное по нему. Например, красный путь на картинке, обозначающей стадион — это круг длиной $$$24$$$.
Соревнование пройдет в $$$q$$$ этапов. На $$$i$$$-м этапе длина круга равна $$$l_i$$$, поэтому организаторам предстоит найти круг для каждого этапа такой, что его длина является делителем $$$l_i$$$. Организаторы не хотят выбирать слишком маленькие круги, поэтому на каждом этапе требуется найти максимальный (по длине) подходящий круг.
Помогите организаторам вычислить максимально возможные длины кругов для всех этапов. Другими словами, для каждого $$$l_i$$$ найдите максимальное целое число $$$L$$$ такое, что $$$l_i \bmod L = 0$$$, и существует круг с длиной ровно $$$L$$$.
Если невозможно выбрать такой круг, то выведите $$$-1$$$.
В первой строке записаны три целых числа $$$n$$$, $$$x$$$ и $$$y$$$ ($$$1 \le n, x, y \le 2 \cdot 10^5$$$, $$$n \le x$$$).
Во второй строке записано $$$n + 1$$$ целое число $$$a_0$$$, $$$a_1$$$, ..., $$$a_n$$$ ($$$0 = a_0 < a_1 < a_2 < \dots < a_{n - 1} < a_n = x$$$).
В третьей строке записано одно целое число $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — количество этапов.
В четвертой строке записаны $$$q$$$ четных целых чисел $$$l_1$$$, $$$l_2$$$, ..., $$$l_q$$$ ($$$4 \le l_i \le 10^6$$$) — длины этапов.
Выведите $$$q$$$ целых чисел. $$$i$$$-е число должно быть равно максимально возможной длине круга для $$$i$$$-го этапа, или $$$-1$$$, если невозможно выбрать круг для данного этапа.
3 10 5 0 3 5 10 6 24 30 14 16 18 10
24 30 14 16 -1 -1
| Название |
|---|




