| Codeforces Round 664 (Div. 1) |
|---|
| Закончено |
No matter what trouble you're in, don't be afraid, but face it with a smile.
I've made another billion dollars!
— Boboniu
Boboniu выпустил свои валюты, под названием Bobo Yuan. Bobo Yuan (BBY) это серия валют. Boboniu присвоил каждой из них положительные целочисленные номера, такие как BBY-1, BBY-2, и так далее.
У Boboniu есть коллекция BBY. Его коллекция выглядит как последовательность. Например:

Мы можем использовать последовательность $$$a=[1,2,3,3,2,1,4,4,1]$$$ длины $$$n=9$$$ чтобы описать ее.
Теперь Boboniu хочет сложить его коллекцию. Вы можете представить, что Boboniu приклеил свою последовательность на длинный лист бумаги и сгибает его между валютами:
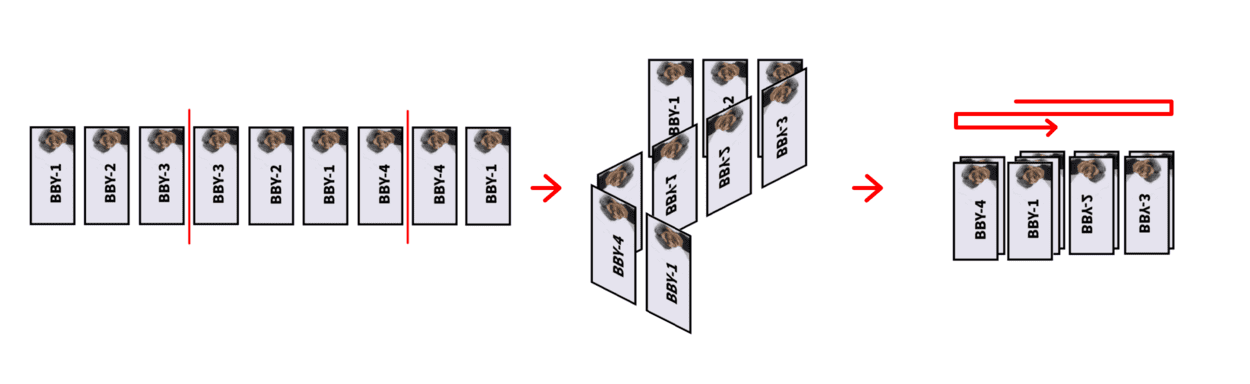
Boboniu будет складывать вместе только валюты с одинаковым номером. Иначе говоря, если $$$a_i$$$ после сгиба находится над $$$a_j$$$ ($$$1\le i,j\le n$$$), то должно выполняться условие $$$a_i=a_j$$$. Boboniu не волнует, выполнялось ли это условие во время сгиба. Но когда сгиб совершен, это условие должно соблюдаться.
Формально определение сгиба описано в примечании.
Согласно картинке выше, вы можете согнуть $$$a$$$ два раза. На самом деле, вы можете согнуть $$$a=[1,2,3,3,2,1,4,4,1]$$$ не более двух раз. Поэтому максимальное число сгибов равно $$$2$$$.
Как международного фаната Boboniu, вас просят найти наибольшее число сгибов.
Вам дана последовательность $$$a$$$ длины $$$n$$$, для каждого $$$i$$$ ($$$1\le i\le n$$$), вам нужно найти наибольшее возможное число сгибов последовательности $$$[a_1,a_2,\ldots,a_i]$$$.
В первой строке записано одно целое число $$$n$$$ ($$$1\le n\le 10^5$$$).
Во второй строке записаны $$$n$$$ целых чисел $$$a_1,a_2,\ldots,a_n$$$ ($$$1\le a_i\le n$$$).
Выведите $$$n$$$ целых чисел. $$$i$$$-е из них должно быть равно максимальному числу сгибов последовательности $$$[a_1,a_2,\ldots,a_i]$$$.
9 1 2 3 3 2 1 4 4 1
0 0 0 1 1 1 1 2 2
9 1 2 2 2 2 1 1 2 2
0 0 1 2 3 3 4 4 5
15 1 2 3 4 5 5 4 3 2 2 3 4 4 3 6
0 0 0 0 0 1 1 1 1 2 2 2 3 3 0
50 1 2 4 6 6 4 2 1 3 5 5 3 1 2 4 4 2 1 3 3 1 2 2 1 1 1 2 4 6 6 4 2 1 3 5 5 3 1 2 4 4 2 1 3 3 1 2 2 1 1
0 0 0 0 1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 4 4 4 5 5 6 7 3 3 3 4 4 4 4 3 3 4 4 4 4 4 5 5 5 5 6 6 6 7 7 8
Формально, для последовательности $$$a$$$ длины $$$n$$$, определим последовательность сгибов как такую последовательность $$$b$$$ длины $$$n$$$, что:
- $$$b_i$$$ ($$$1\le i\le n$$$) равно $$$1$$$ или $$$-1$$$.
- Определим $$$p(i)=[b_i=1]+\sum_{j=1}^{i-1}b_j$$$. Для всех $$$1\le i<j\le n$$$, если $$$p(i)=p(j)$$$, то $$$a_i$$$ должно быть равно $$$a_j$$$.
($$$[A]$$$ это значение логического выражения $$$A$$$. т.е. $$$[A]=1$$$ если $$$A$$$ истинно, иначе $$$[A]=0$$$).
Определим количество сгибов $$$b$$$ как $$$f(b)=\sum_{i=1}^{n-1}[b_i\ne b_{i+1}]$$$.
Максимальное количество сгибов $$$a$$$ это $$$F(a)=\max\{ f(b)\mid b \text{ является последовательностью сгибов }a \}$$$.
| Название |
|---|




