| Codeforces Round 664 (Div. 1) |
|---|
| Закончено |
У Boboniu есть ориентированный граф с $$$n$$$ вершинами и $$$m$$$ ребрами.
Исходящая степень каждой вершины не превосходит $$$k$$$.
У каждого ребра есть целочисленный вес от $$$1$$$ до $$$m$$$. Никакие два ребра не имеют одинаковый вес.
Boboniu любит ходить по графу придерживаясь определенных правил, которые задаются последовательностью $$$(c_1,c_2,\ldots,c_k)$$$. Если в текущий момент он стоит в вершине $$$u$$$ с исходящей степени $$$i$$$, тогда после этого он перейдет в вершину по ребру с $$$c_i$$$-м $$$(1\le c_i\le i)$$$ номером в отсортированном по весу порядке среди всех ребер исходящих из $$$u$$$.
Boboniu попросил вас посчитать число таких последовательностей $$$(c_1,c_2,\ldots,c_k)$$$, что:
- $$$1\le c_i\le i$$$ для всех $$$i$$$ ($$$1\le i\le k$$$).
- Начав с любой вершины $$$u$$$, возможно вернуться обратно в $$$u$$$ за конечное время передвигаясь по графу по описанным правилам.
В первой строке записаны три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$2\le n\le 2\cdot 10^5$$$, $$$2\le m\le \min(2\cdot 10^5,n(n-1) )$$$, $$$1\le k\le 9$$$).
Каждая из следующих $$$m$$$ строк содержит три целых числа $$$u$$$, $$$v$$$ и $$$w$$$ $$$(1\le u,v\le n,u\ne v,1\le w\le m)$$$, описывающих ребро из $$$u$$$ в $$$v$$$ с весом $$$w$$$. Гарантируется, что в графе нет петель и кратных ребер, и из каждой вершины исходит хотя бы одно ребро.
Гарантируется, что исходящая степень каждой вершины не превышает $$$k$$$ и никакие два ребра не имеют одинаковый вес.
Выведите одно целое число: количество последовательностей.
4 6 3 4 2 1 1 2 2 2 4 3 4 1 4 4 3 5 3 1 6
2
5 5 1 1 4 1 5 1 2 2 5 3 4 3 4 3 2 5
1
6 13 4 3 5 1 2 5 2 6 3 3 1 4 4 2 6 5 5 3 6 4 1 7 4 3 8 5 2 9 4 2 10 2 1 11 6 1 12 4 6 13
1
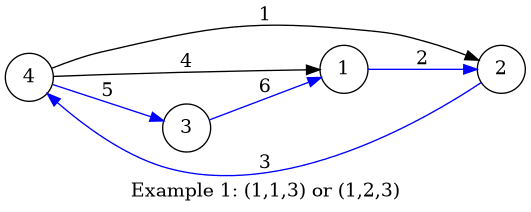
В первом примере есть две последовательности: $$$(1,1,3)$$$ и $$$(1,2,3)$$$. Синие ребра обозначают $$$c_i$$$-е по весу ребра, по которым решил ходить Boboniu.
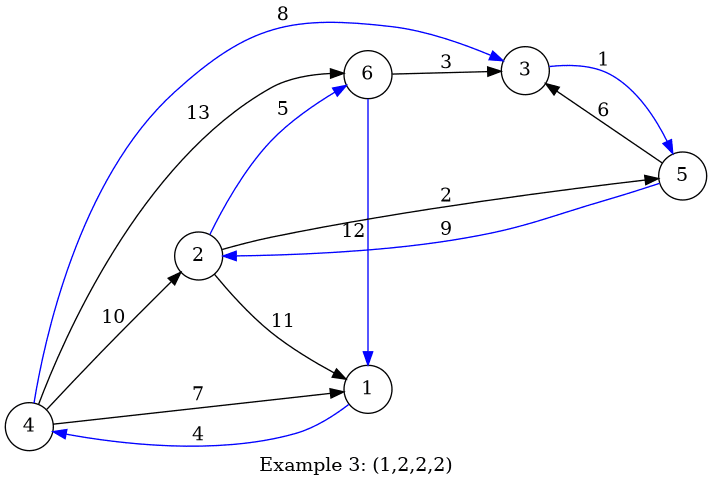
Для третьего примера есть только одна последовательность: $$$(1,2,2,2)$$$.
Исходящая степень вершины $$$u$$$ это количество ребер исходящих из $$$u$$$.
| Название |
|---|




