| Codeforces Round 662 (Div. 2) |
|---|
| Закончено |
Одним вечером Радуга и Флаттершай придумали игру. Так как пони дружат, то и в игре они решили не соревноваться, а вместе двигаться к общей цели.
Игра начинается на квадратном плоском поле, у которого изначально выложены внешние границы. У Радуги и Флаттершай есть квадратные плоские фишки размера $$$1\times1$$$, у Радуги бесконечное число голубых фишек, у Флаттершай бесконечное число желтых фишек.
Фишки выкладываются по следующему правилу: каждая новая выкладываемая фишка должна соприкасаться стороной с уже построенной фигурой (внешняя граница игрового поля считается построенной изначально). На очередном ходу одна пони может выложить любое количество фишек своего цвета в соответствие с правилами игры.
Радуга и Флаттершай догадались, что таким образом можно выкладывать различные узоры на игровом поле. Они решили начать с чего-то простого, поэтому решили выложить фишки так, чтобы они образовали шахматную раскраску. Радуга славится своей скоростью, поэтому ей стало интересно, за какое минимальное количество ходов они с Флаттершай смогут получить шахматную раскраску, закрыв все поле фишками. Помогите ей найти это количество!
Так как пони могут играть много раз на разных досках, Радуга просит найти минимальное количество ходов для нескольких игровых полей.
Напоминаем, что шахматная раскраска поля в два цвета — та, в которой любая клетка соседствует по стороне только с клетками другого цвета.
Первая строка содержит одно целое число $$$T$$$ ($$$1 \le T \le 100$$$) — количество игровых полей. Каждая из следующих $$$T$$$ строк содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^9$$$) — сторона поля.
Для каждого игрового поля выведите минимальное количество ходов, чтобы выложить на нем шахматную раскраску из фишек.
2 3 4
2 3
Для поля $$$3\times3$$$ пони могут сделать два следующих хода: 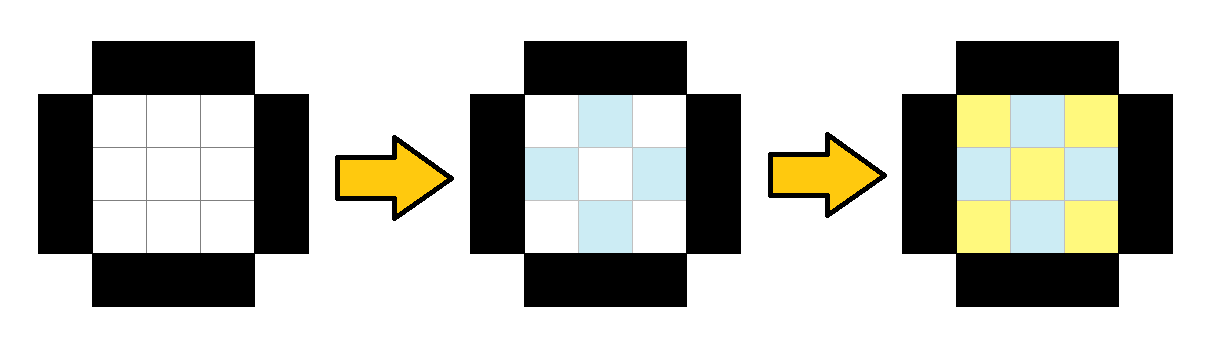
| Название |
|---|




