Пусть $$$a$$$ и $$$b$$$ будут некоторыми неотрицательными целыми числами. Определим странное сложение $$$a$$$ и $$$b$$$ следующим образом:
- запишем числа одно под другим и выровняем их по младшему разряду;
- сложим числа поразрядно и запишем полученные суммы одну за другой.
Будем считать, что у обоих чисел бесконечное число лидирующих нулей.
Например, взглянем на странное сложение чисел $$$3248$$$ и $$$908$$$:
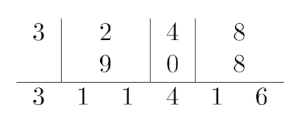
Вам задана строка $$$c$$$, состоящая из $$$n$$$ цифр от $$$0$$$ до $$$9$$$. Также заданы $$$m$$$ запросов обновления следующего вида:
- $$$x~d$$$ — заменить цифру на $$$x$$$-й позиции $$$c$$$ на цифру $$$d$$$.
Обратите внимание, что $$$c$$$ может иметь лидирующие нули в любой момент времени.
После каждого обновления выведите количество пар чисел $$$(a, b)$$$ таких, что $$$a$$$ и $$$b$$$ оба являются неотрицательными целыми числами и результат странного сложения $$$a$$$ и $$$b$$$ равен $$$c$$$.
Обратите внимание, что количество пар может быть довольно велико, поэтому требуется вывести его по модулю $$$998244353$$$.
В первой строке записано два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 5 \cdot 10^5$$$) — длина числа $$$c$$$ и количество запросов обновления.
Во второй строке задана строка $$$c$$$, состоящая из ровно $$$n$$$ цифр от $$$0$$$ до $$$9$$$.
В каждой из следующих $$$m$$$ строк записаны по два целых числа $$$x$$$ и $$$d$$$ ($$$1 \le x \le n$$$, $$$0 \le d \le 9$$$) — описания запросов обновления.
Выведите $$$m$$$ целых чисел — $$$i$$$-е значение должно быть равно количеству пар чисел $$$(a, b)$$$ таких, что $$$a$$$ и $$$b$$$ оба являются неотрицательными целыми числами и результат странного сложения $$$a$$$ и $$$b$$$ равен $$$c$$$ после применения $$$i$$$ запросов обновления.
Обратите внимание, что количество пар может быть довольно велико, поэтому требуется вывести его по модулю $$$998244353$$$.
2 3 14 2 4 2 1 1 0
15 12 2
После первого запроса $$$c$$$ равно $$$14$$$. Пары, которые складываются в $$$14$$$: $$$(0, 14)$$$, $$$(1, 13)$$$, $$$(2, 12)$$$, $$$(3, 11)$$$, $$$(4, 10)$$$, $$$(5, 9)$$$, $$$(6, 8)$$$, $$$(7, 7)$$$, $$$(8, 6)$$$, $$$(9, 5)$$$, $$$(10, 4)$$$, $$$(11, 3)$$$, $$$(12, 2)$$$, $$$(13, 1)$$$, $$$(14, 0)$$$.
После второго запроса $$$c$$$ равно $$$11$$$.
После третьего запроса $$$c$$$ равно $$$01$$$.
| Название |
|---|




