| Codeforces Global Round 9 |
|---|
| Закончено |
Вам дано дерево с $$$n$$$ вершинами. Вы можете изменить строение дерева с помощью следующей многошаговой операции:
- Выберите три вершины $$$a$$$, $$$b$$$ и $$$c$$$ такие, чтобы $$$b$$$ соединена ребром и с $$$a$$$ и с $$$c$$$.
- Для каждой вершины $$$d$$$ кроме $$$b$$$, которая соединена ребром с $$$a$$$, удалите ребро, соединяющее $$$d$$$ и $$$a$$$, и добавьте ребро, соединяющее $$$d$$$ и $$$c$$$.
- Удалите ребро, соединяющее $$$a$$$ и $$$b$$$, и добавьте ребро, соединяющее $$$a$$$ и $$$c$$$.
В качестве примера рассмотрим следующее дерево:
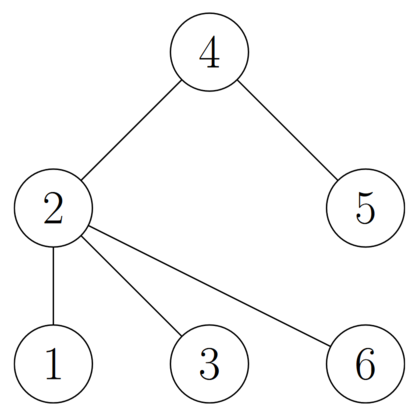
Следующая диаграмма иллюстрирует последовательность шагов, которые происходят, когда мы применяем операцию к вершинам $$$2$$$, $$$4$$$ и $$$5$$$:
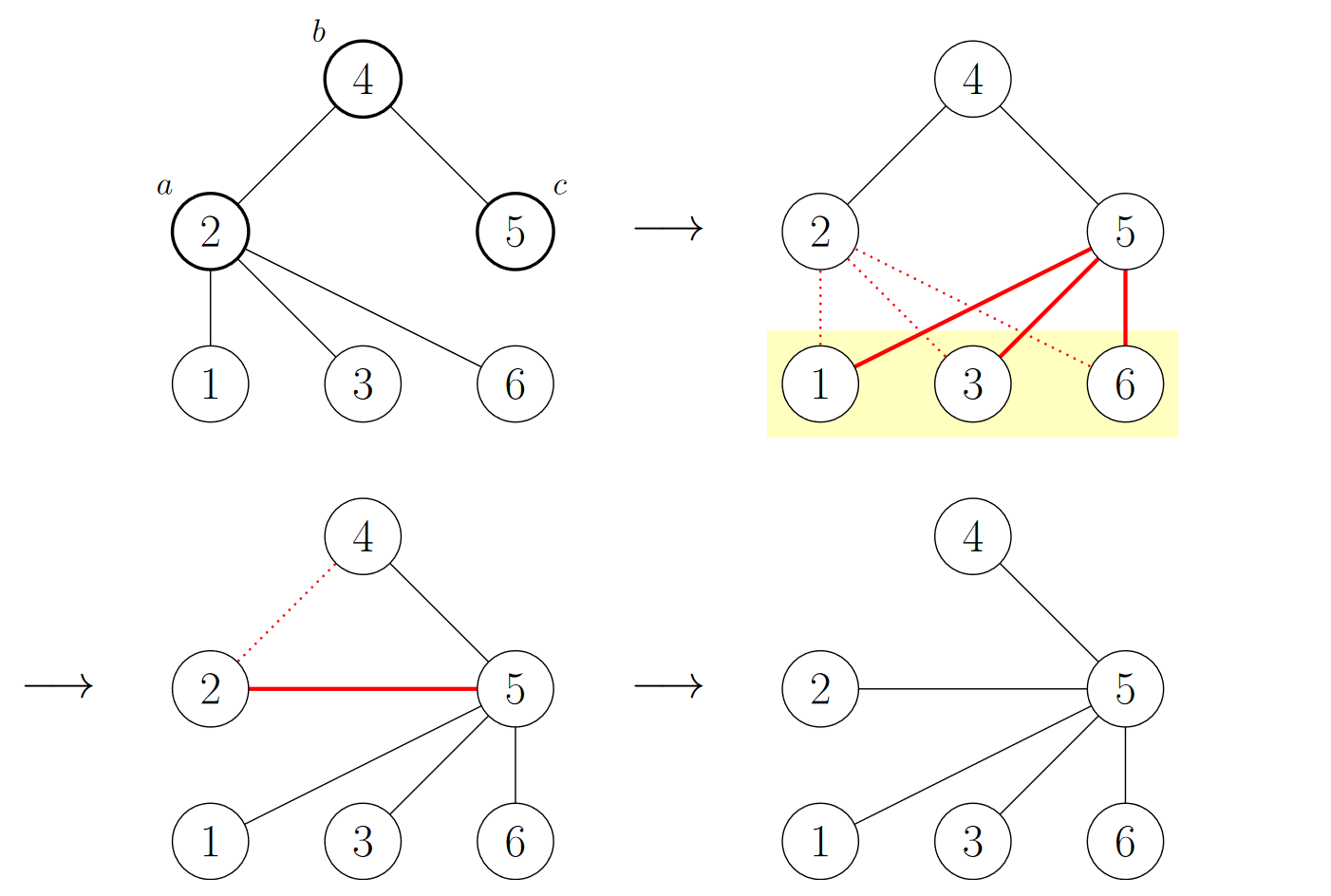
Можно доказать, что после каждой операции полученный граф все еще является деревом.
Найдите минимальное количество операций, которые необходимо выполнить, чтобы превратить дерево в звезду. Звезда — это дерево с одной вершиной степени $$$n - 1$$$, называемой его центром, и $$$n - 1$$$ вершинами степени $$$1$$$.
Первая строка содержит целое число $$$n$$$ ($$$3 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
$$$i$$$-я из следующих $$$n - 1$$$ строк содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$), обозначающих существование ребра, соединяющего вершины $$$u_i$$$ и $$$v_i$$$. Гарантируется, что данные ребра образуют дерево.
Выведите единственное целое число — минимальное количество операций, необходимое для преобразования дерева в звезду.
Можно доказать, что при данных ограничениях всегда можно превратить дерево в звезду, используя не более $$$10^{18}$$$ операций.
6 4 5 2 6 3 2 1 2 2 4
1
4 2 4 4 1 3 4
0
Первый пример соответствует дереву из условия. Как мы уже видели, мы можем превратить дерево в звезду с центром в вершине $$$5$$$, применив одну операцию к вершинам $$$2$$$, $$$4$$$ и $$$5$$$.
Во втором тестовом примере данное дерево уже является звездой с центром в вершине $$$4$$$, поэтому никаких операций выполнять не нужно.
| Название |
|---|




