| Codeforces Global Round 8 |
|---|
| Закончено |
Лео-младший рисует в тетради в клеточку (каждая страница размечена квадратной сеткой). Можно считать, что страницы бесконечно большие в любом направлении.
Лео-младший закрашивает некоторые клетки на странице серым цветом. Он считает получившийся рисунок красивым, если выполнены следующие условия:
- Рисунок связен, то есть, из любой серой клетки можно попасть в любую другую по цепочке из серых клеток, в которой каждые две последовательные клетки — соседи (то есть, имеют общую сторону).
- Каждая серая клетка имеет чётное количество серых соседей.
- В рисунке ровно $$$n$$$ серых клеток, у которых все соседи серые. Количество остальных серых клеток может произвольным (но разумным, чтобы их можно было перечислить).
Лео-младший пытается нарисовать красивый рисунок для выбранного значения $$$n$$$. Помогите ему, найдите любой пример красивого рисунка.
Чтобы вывести координаты клеток в ответе, предполагайте, что на странице введена декартова система координат, в которой одна из клеток является началом координат $$$(0, 0)$$$, оси $$$0x$$$ и $$$0y$$$ перпендикулярны и сонаправлены линиям сетки, и шаг единичной длины в любом направлении вдоль любой оси ведёт в соседнюю клетку.
В единственной строке записано одно целое число $$$n$$$ ($$$1 \leq n \leq 500$$$) — количество серых клеток, у которых все соседи серые.
В первой строке выведите одно целое число $$$k$$$ — количество серых клеток в вашем рисунке. По техническим причинам $$$k$$$ не должно превосходить $$$5 \cdot 10^5$$$.
Каждая из следующих $$$k$$$ строк должна содержать две целых числа — координаты очередной серой клетки в вашем рисунке. Все перечисленные клетки должны быть различны, и рисунок должен отвечать всем требованиям, перечисленным выше. Все координаты не должны превосходить $$$10^9$$$ по абсолютной величине.
Можно показать, что существует ответ, который удовлеторяет всем требованиям и укладывается в ограничение на $$$k$$$.
4
12 1 0 2 0 0 1 1 1 2 1 3 1 0 2 1 2 2 2 3 2 1 3 2 3
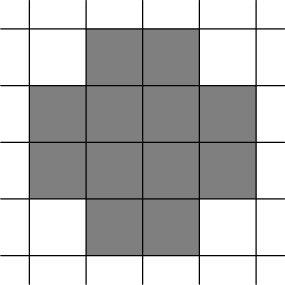
Ответ для примера изображен ниже:
| Название |
|---|




