| Codeforces Round 639 (Div. 1) |
|---|
| Закончено |
Все верно. Я студент университета Пердью и безо всякого стыда придумал задачу про поезда.
Есть $$$n$$$ станций и $$$m$$$ поездов. Станции соединяются $$$n-1$$$ однонаправленной железной дорогой так, что они образуют корневое дерево с корнем в станции $$$1$$$. Все железные дороги имеют направлены вдоль путей от корневой станции $$$1$$$ к листьям. Каждая железная дорога ведет от станции $$$u$$$ к станции $$$v$$$ и имеет расстояние $$$d$$$, обозначающее, что требуется $$$d$$$ единиц времени, чтобы доехать от станции $$$u$$$ к станции $$$v$$$. Каждая станция, из которой выходит хотя бы одна железная дорога, имеет переключатель, который определяет станцию, в которую затем поедет любой поезд, приехавший на эту станцию. Например, это может выглядеть следующим образом:
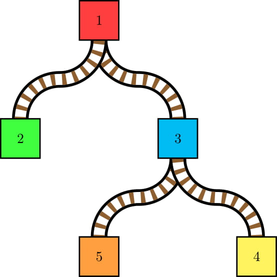Здесь станции $$$1$$$ и $$$3$$$ имеют переключатели, направляющие к станциям $$$2$$$ и $$$4$$$, соответственно. Изначально ни на одной станции нет поезда. Поезд $$$i$$$ появится на станции $$$1$$$ в момент времени $$$t_i$$$. В каждый момент времени, начиная с $$$1$$$, будут происходить следующие два шага:
- Вы можете переключить переключатель не более одной станции на другую дорогу, выходящую из этой станции. Переключение происходит до шага $$$2$$$.
- Любой поезд, который находится на станции $$$u$$$, направляется к станции $$$v$$$, в которую указывает переключатель станции $$$u$$$. Если железная дорога от станции $$$u$$$ к станции $$$v$$$ имела расстояние $$$d$$$, поезд прибудет на станцию $$$v$$$ через $$$d$$$ единиц времени от настоящего момента.
У каждого поезда есть станция прибытия $$$s_i$$$. Когда он прибывает на станцию $$$s_i$$$, он останавливается там навсегда. Если в какой-то момент времени поезд поедет в неверном направлении, то есть он никогда уже не сможет достичь станции $$$s_i$$$ независимо от состояния переключателей, он тут же взорвется.
Найдите наибольшее возможное время первого взрыва, если вы будете переключать переключатели оптимально или определите, что вы можете направить каждый поезд к своей станции прибытия так, что ни одного взрыва не произойдет. Также найдите минимальное количество переключений, которое требуется, чтобы достичь этого.
В первой строке находятся два целых числа $$$n$$$ и $$$m$$$ ($$$1\le n,m\le 10^5$$$) — количество станций и поездов, соответственно.
Следующие $$$n-1$$$ строк описывают железные дороги. $$$i$$$-я из этих строк содержит три целых числа $$$u,v,d$$$ ($$$1\le u,v\le n$$$, $$$1\le d\le 10^9$$$), обозначающие железную дорогу от станции $$$u$$$ к станции $$$v$$$, имеющую расстояние $$$d$$$. Гарантируется, что железные дороги формируют корневое дерево с корнем в станции $$$1$$$. Переключатель в станции $$$u$$$ изначально направлен вдоль последней в данном порядке железной дороги, выходящей из станции $$$u$$$.
Следующие $$$m$$$ строк описывают поезда. $$$i$$$-я из этих строк содержит два целых числа $$$s_i,t_i$$$ ($$$1\le s_i\le n$$$, $$$1\le t_1<t_2<\cdots<t_m\le 10^9$$$) — станция назначения и время, в которое $$$i$$$-й поезд прибудет на станцию $$$1$$$, соответственно.
Выведите два целых числа: наибольшее возможное время первого взрыва (или $$$-1$$$, если можно предотвратить взрывы) и минимальное количество переключений, необходимое, чтобы достичь этого.
5 4 1 2 1 1 3 2 3 4 1 3 5 3 2 1 4 2 2 6 5 10
-1 6
5 4 1 2 1 1 3 2 3 4 1 3 5 3 5 1 4 2 4 3 2 4
4 0
11 6 1 2 1 1 3 2 3 4 1 3 5 2 5 6 1 5 7 2 7 8 1 7 9 2 9 10 1 9 11 1 2 1 8 3 6 5 10 7 4 9 2 11
11 4
В первом тесте один из возможных примеров того, как все будет происходить, описан ниже.
- В момент времени $$$1$$$ поезд $$$1$$$ прибывает на станцию $$$1$$$. Переключатель станции $$$1$$$ направлен к станции $$$2$$$. Поезд $$$1$$$ отправляется к станции $$$2$$$.
- В момент времени $$$2$$$ поезд $$$2$$$ прибывает на станцию $$$1$$$ и поезд $$$1$$$ прибывает на станцию $$$2$$$, где останавливается навсегда. Мы переключаем переключатель в станции $$$1$$$ к станции $$$3$$$. Поезд $$$2$$$ направляется к станции $$$3$$$.
- В момент времени $$$4$$$ поезд $$$2$$$ прибывает на станцию $$$3$$$. Мы переключаем переключатель в станции $$$3$$$ к станции $$$4$$$. Поезд $$$2$$$ направляется к станции $$$4$$$.
- В момент времени $$$5$$$ поезд $$$2$$$ прибывает на станцию $$$4$$$, где останавливается навсегда.
- В момент времени $$$6$$$ поезд $$$3$$$ прибывает на станцию $$$1$$$. Мы переключаем переключатель станции $$$1$$$ к станции $$$2$$$. Поезд $$$3$$$ направляется к станции $$$2$$$.
- В момент времени $$$7$$$ поезд $$$3$$$ прибывает на станцию $$$2$$$, где останавливается навсегда. Мы переключаем переключатель станции $$$3$$$ к станции $$$5$$$.
- В момент времени $$$10$$$ поезд $$$4$$$ прибывает на станцию $$$1$$$. Мы переключаем переключатель станции $$$1$$$ к станции $$$3$$$. Поезд $$$4$$$ направляется к станции $$$3$$$.
- В момент времени $$$12$$$ поезд $$$4$$$ прибывает на станцию $$$3$$$. Поезд $$$4$$$ направляется к станции $$$5$$$.
- В момент времени $$$15$$$ поезд $$$4$$$ прибывает на станцию $$$5$$$, где останавливается навсегда.
Во втором тесте мы не переключаем ничего. В момент времени $$$4$$$ поезд $$$2$$$ направляется к станции $$$5$$$, и поезд $$$4$$$ направляется к станции $$$3$$$. Они оба взрываются. Невозможно предотвратить взрывы поездов к моменту времени $$$4$$$.
В третьем тесте давайте будем обозначать переключение переключателя как $$$(u\to v,t)$$$, если мы переключаем переключатель станции $$$u$$$ к станции $$$v$$$ в момент времени $$$t$$$. Одним из решений является сделать следующие $$$4$$$ переключения: $$$(1\to 2,1)$$$, $$$(1\to 3,2)$$$, $$$(7\to 8,5)$$$, $$$(5\to 6,8)$$$. В момент времени $$$11$$$ поезда $$$4$$$, $$$5$$$ и $$$6$$$ взорвутся. Невозможно предотвратить взрывы поездов к моменту времени $$$11$$$.
