К сожалению, была найдена ошибка в доказательстве авторского решения этой задачи. На данный момент нам неизвестно абсолютно верное решение. Тем не менее, вы можете сдавать эту задачу, но в случае, если ваше решение пройдет все тесты, оно не будет гарантированно верным. Если ваше решение прошло все тесты и вы уверены в доказательстве его корректности, вы можете написать одному из авторов соревнования об этом.
Наверняка вы все читали книгу «Алиса в стране чудес». В этой задаче Настя оказалась в стране Трёх странных Пчёл. Пчёлы странные, потому что их соты пятиугольные. Настя пробралась туда незаконно, поэтому она хочет, чтобы вы её не поймали. Помогите пчёлам наказать нарушительницу!
Это интерактивная задача.
Пчелиный улей представляет собой связный неориентированный граф, по ребрам которого могут перемещаться пчелы и Настя. Граф удовлетворяет двум свойствам:
- Степень любой его вершины не больше чем $$$3$$$.
- Для каждого ребра существует цикл длины не больше чем $$$5$$$, проходящий через это ребро.
Есть три пчелы и Настя. Вы играете за пчел. Сначала вы выбираете вершины, в которые поставите пчел. Затем Настя выбирает вершину, в которой она изначально окажется. Один ход представляет из себя перемещения сначала пчел, потом Насти, по очереди:
- Для каждой из ваших пчел, вы можете либо переместить каждую ее по какому-нибудь ребру графа, выходящему из вершины, где находится эта пчела или оставить ее на месте.
- Затем Настя обязательно перемещается по какому-нибудь ребру графа, выходящему из вершины, в которой она сейчас находится.
Вы побеждаете, если хотя бы одна из пчел и Настя оказываются в одной вершине в любой момент игры.
Если после $$$n$$$ ходов такая ситуация не происходит, то вы проигрываете.
Несколько пчел могут находиться в одной и той же вершине.
В первой строке даны два целых числа $$$n$$$ $$$(4 \leq n \leq 5000)$$$ и $$$m$$$ $$$(n \leq m \leq 3n)$$$ — количество вершин и рёбер в графе.
Каждая из следующих $$$m$$$ строк содержит по два целых числа $$$v$$$ и $$$u$$$ $$$(1 \leq v, u \leq n)$$$, которые означают, что между вершинами $$$v$$$ и $$$u$$$ есть ребро. Гарантируется, что граф связен, не содержит петель, что степень любой вершины не превосходит $$$3$$$ и через каждое ребро проходит цикл длины не больше чем $$$5$$$. Обратите внимание, граф может содержать кратные рёбра.
На каждом ходу вы должны выводить ровно по три вершины $$$a, b, c$$$ $$$(1 \leq a, b, c \leq n)$$$. В первый раз выведенные $$$3$$$ вершины будут означать, в какие вершины вы изначально поставили пчел. В ответ вы получите вершину, в которую жюри расположило Настю. Каждые следующие $$$3$$$ вершины будут означать, где оказываются $$$3$$$ пчелы после вашего хода. Каждая из пчел может независимо от других пчел как остаться в текущей вершине, так и переместиться по ребру. После очередного вывода $$$3$$$ вершин, в ответ вы получаете номер новой вершины, в которую пошла Настя.
Как только одна из пчёл оказалась в одной вершине с Настей или вы достигли лимита на количество ходов, ваша программа должна завершить работу. То есть, если вы сделали ход, и одна из пчел оказалась в одной вершине с Настей, ваша программа должна завершить работу, либо если Настя сделала ход и оказалась в одной вершине с одной из пчел, вы не должны делать свой ход и программа должна завершить работу.
При превышении лимита на количество ходов (то есть количество ваших ходов превысило $$$n$$$, где $$$n$$$ — количество вершин в графе) будет ваша программа получит вердикт неправильный ответ, в случае немедленного завершения.
Ваше решение может получить вердикт Решение «зависло», если вы ничего не выведете или забудете сбросить буфер вывода.
Чтобы сбросить буфер вывода вам нужно сделать следующее сразу после вывода запроса и символа конца строки:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- см. документацию других языков.
В этой задаче интерактор адаптивный. Это означает, что в зависимости от всех ваших предыдущих ходов поведение Насти может изменяться.
Взломы недоступны для этой задачи.
5 5 1 2 2 3 3 4 4 5 5 1 4 5
1 1 2 1 5 3
8 9 1 2 2 3 3 4 4 5 5 1 5 6 6 7 7 8 8 4 1 5
7 3 3 6 2 2 5 3 1
Пусть Настя - это зелёная фишка, а три пронумерованных красных - это три пчелы.
В первом тесте перемещение героев выглядит так.
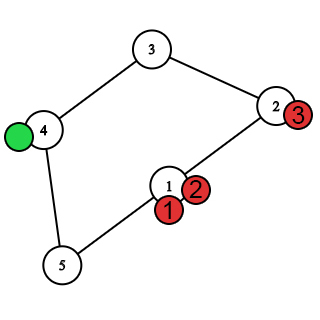 После выбора стартовых вершин.
После выбора стартовых вершин. 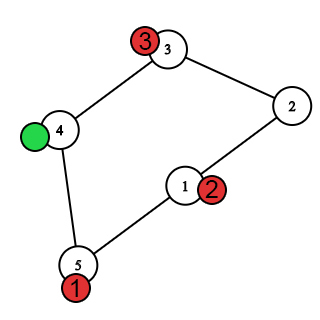 Первых ход после перемещения пчёл.
Первых ход после перемещения пчёл. 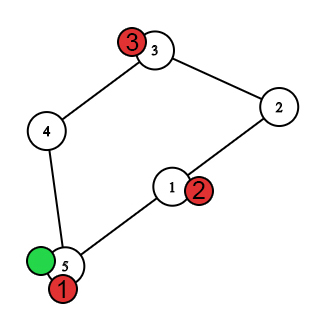 Первых ход после перемещения Насти. Настя поймана пчелой 1.
Первых ход после перемещения Насти. Настя поймана пчелой 1. Во втором тесте перемещение героев выглядит так.
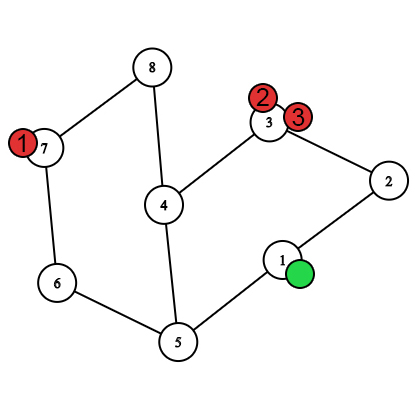 После выбора стартовых вершин.
После выбора стартовых вершин. 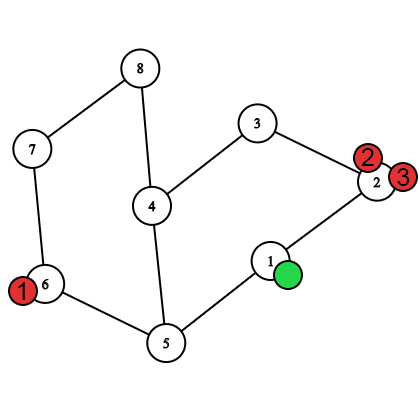 Первых ход после перемещения пчёл.
Первых ход после перемещения пчёл. 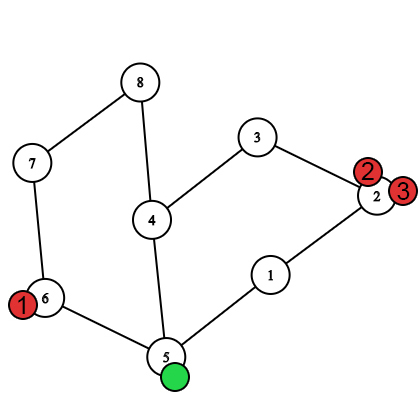 Первых ход после перемещения Насти.
Первых ход после перемещения Насти. 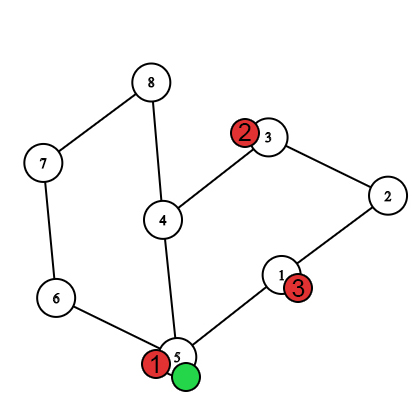 Второй ход после перемещения пчёл. Настя поймана пчелой 1.
Второй ход после перемещения пчёл. Настя поймана пчелой 1.
| Название |
|---|




