Денис, справившийся с покупкой цветов и конфет (об этой истории вы узнаете в следующей задаче), поехал на встречу с Настей, чтобы предложить ей стать парой.
И вот, они сидят вместе в кафе, болтают. Решительный Денис наконец-то предлагает быть им вместе, но... Но Настя не даёт никакого ответа.
Как же сильно расстроился бедный парень. Так сильно, что он пнул какое-то табло с цифрами. Цифры отображаются таким же образом, как на электронных часах: каждая позиция для цифры состоит из $$$7$$$ сегментов, которые могут быть включены или выключены, чтобы отображать различные цифры. На картинке показано, как изображаются все $$$10$$$ десятичных цифр:

Разрешается, чтобы в числе были лидирующие нули.
В первой строке дано число $$$n$$$ $$$(1 \leq n \leq 2000)$$$ — количество цифр на табло и $$$k$$$ $$$(0 \leq k \leq 2000)$$$ — количество сломанных палочек.
В следующих $$$n$$$ строках находится по одной бинарной строке длины $$$7$$$, $$$i$$$-я из которых кодирует $$$i$$$-ю цифру табло.
Каждая цифра на табло состоит из $$$7$$$ палочек. Пронумеруем их, как на картинке ниже, и пусть на $$$i$$$-м месте бинарной строки будет $$$0$$$, если $$$i$$$-я палочка не горит и $$$1$$$, если горит. Тогда бинарная строка длины $$$7$$$ будет задавать то, какие палочки горят.
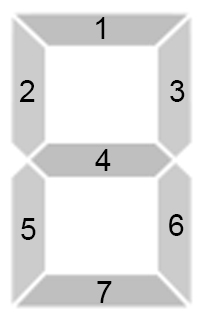
Таким образом, последовательности «1110111», «0010010», «1011101», «1011011», «0111010», «1101011», «1101111», «1010010», «1111111», «1111011» кодируют по порядку все цифры от $$$0$$$ до $$$9$$$ включительно.
Выведите единственное число, состоящее из $$$n$$$ разрядов – максимальное число, которое можно получить, если включить ровно $$$k$$$ палочек или $$$-1$$$, если невозможно так включить ровно $$$k$$$ палочек, чтобы на табло получилась какая-то последовательность цифр.
1 7 0000000
8
2 5 0010010 0010010
97
3 5 0100001 1001001 1010011
-1
В первом тесте мы обязаны включить все $$$7$$$ палочек и получить на табло одну цифру $$$8$$$.
Во втором тесте у нас включены палочки таким образом, что образуются единицы. За $$$5$$$ дополнительно включённых палочек можно получить числа $$$07$$$, $$$18$$$, $$$34$$$, $$$43$$$, $$$70$$$, $$$79$$$, $$$81$$$ и $$$97$$$, из них выбираем максимальное — $$$97$$$.
В третьем тесте невозможно так включить ровно $$$5$$$ палочек, чтобы на табло получилась какая-то последовательность цифр.
| Название |
|---|




