| Codeforces Round 633 (Div. 1) |
|---|
| Закончено |
У вас есть дерево из $$$n$$$ вершин. Вы собираетесь преобразовать это дерево в $$$n$$$ резинок на бесконечной плоскости. Должно выполняться следующее;
- Для каждой пары вершин $$$a$$$ и $$$b$$$, резинки $$$a$$$ и $$$b$$$ должны пересекаться тогда и только тогда, когда между $$$a$$$ и $$$b$$$ в дереве существует ребро.
- Форма резинки должна быть простой петлей. Другими словами, резинка — это замкнутая кривая без самопересечений.
Теперь давайте дадим следующие определения:
- Резинка $$$a$$$ включает резинку $$$b$$$, если и только если резинка $$$b$$$ находится полностью внутри резинки $$$a$$$, и они не пересекаются.
- Последовательность резинок $$$a_{1}, a_{2}, \ldots, a_{k}$$$ ($$$k \ge 2$$$) называется вложенной, если и только если для всех $$$i$$$ ($$$2 \le i \le k$$$), $$$a_{i-1}$$$ включает в себя $$$a_{i}$$$.
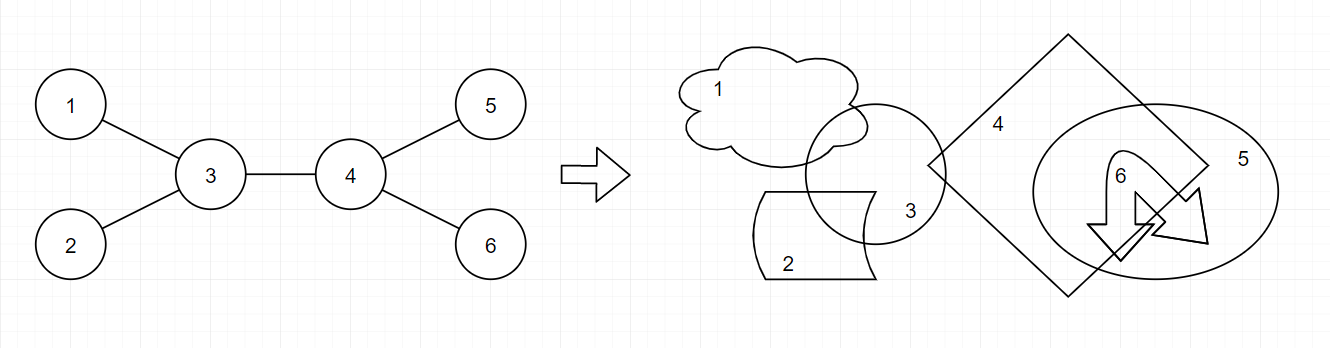 Это пример преобразования. Обратите внимание, что резинки $$$5$$$ и $$$6$$$ являются вложенными.
Это пример преобразования. Обратите внимание, что резинки $$$5$$$ и $$$6$$$ являются вложенными. Можно доказать, что при заданных ограничениях существует преобразование и последовательность вложенных резинок.
Какую максимальную длину последовательности вложенных резинок можно получить из данного дерева? Найдите и выведите ее.
Первая строка содержит целое число $$$n$$$ ($$$3 \le n \le 10^{5}$$$) — количество вершин в данном дереве.
$$$i$$$-я из следующих $$$n-1$$$ строк содержит два целых числа $$$a_{i}$$$ и $$$b_{i}$$$ ($$$1 \le a_{i} \lt b_{i} \le n$$$) — это означает, что существует ребро между $$$a_{i}$$$ и $$$b_{i}$$$. Гарантируется, что данный граф образует дерево из $$$n$$$ вершин.
Выведите ответ.
6 1 3 2 3 3 4 4 5 4 6
4
4 1 2 2 3 3 4
2
В первом примере можно получить вложенную последовательность из $$$4$$$ резинок ($$$1$$$, $$$2$$$, $$$5$$$ и $$$6$$$) с помощью следующего преобразования, приведенного ниже. Конечно, существуют и другие преобразования для создания вложенной последовательности длины $$$4$$$. Однако вы не можете сделать последовательность из $$$5$$$ или более вложенных резинок для данного дерева.
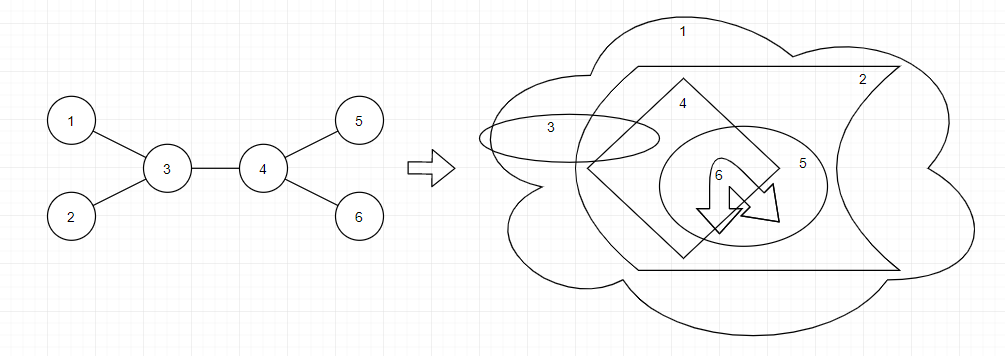
Одно из возможных преобразований для второго примера приведено ниже.
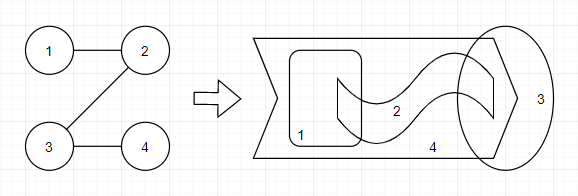
| Название |
|---|




