| Codeforces Round 635 (Div. 1) |
|---|
| Закончено |
Написание легких романов является очень важной частью жизни Linova. Прошлой ночью ей приснилось сказочное королевство. Linova написала легкий роман про это королевство, как только проснулась. Конечно, она стала его королевой.

Всего есть $$$n$$$ городов и $$$n-1$$$ двусторонняя дорога, соединяющая некоторые пары городов королевства. Из любого города вы можете попасть в любой другой город, пройдя по некоторым дорогам. Города пронумерованы от $$$1$$$ до $$$n$$$ и город $$$1$$$ является столицей королевства. Таким образом, структура королевства является деревом.
Как королева, Linova планирует выбрать ровно $$$k$$$ городов для развития индустрии, тогда как в остальных городах будет развиваться туризм. Столица также может быть как индустриальным, так и туристическим городом.
Раз в год в столице будет проходить встреча. Для участия во встрече, каждый индустриальный город посылает участника. Все посланники приедут в столицу по кратчайшему пути (который как известно единственный в дереве).
Путешествие по туристическим городам очень приятно. Для каждого посланника, его уровень счастья равен количеству туристических городов на его пути.
Для того, чтобы люди любили королеву, Linova хочет выбрать $$$k$$$ городов так, чтобы максимизировать сумму уровней счастья всех посланников. Можете ли вы посчитать максимальную возможную сумму для нее?
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$2\le n\le 2 \cdot 10^5$$$, $$$1\le k< n$$$) — количество городов и индустриальных городов, соответственно.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1\le u,v\le n$$$), обозначающих наличие дороги, соединяющей города $$$u$$$ и $$$v$$$.
Гарантируется, что из любого города можно достичь любой другой по дорогам.
Выведите строку, содержащую единственное целое число — максимальную возможную сумму уровней счастья всех посланников, которую можно достичь.
7 4 1 2 1 3 1 4 3 5 3 6 4 7
7
4 1 1 2 1 3 2 4
2
8 5 7 5 1 7 6 1 3 7 8 3 2 1 4 5
9
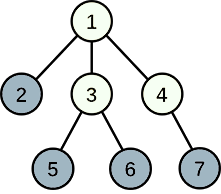
В первом тесте, Linova может выбрать города $$$2$$$, $$$5$$$, $$$6$$$, $$$7$$$ для развития индустрии, тогда уровень счастья посланника из города $$$2$$$ будет равен $$$1$$$, уровни счастья посланников из городов $$$5$$$, $$$6$$$, $$$7$$$ будут равны $$$2$$$. Таким образом, сумма уровней счастья будет равна $$$7$$$ и можно доказать, что это максимальная возможная сумма, которая может быть.
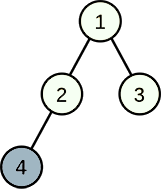
Во втором тесте, выбрав города $$$3$$$ и $$$4$$$ для развития индустрии можно достичь суммы $$$3$$$, но обратите внимание, что Linova планирует выбрать ровно $$$k$$$ городов для развития индустрии, поэтому максимальная сумма равна $$$2$$$.
| Название |
|---|




