| Codeforces Round 630 (Div. 2) |
|---|
| Закончено |
Алиса недавно подсела на игру, которая называется Сиртет.
В игре Сиртет игроку дается поле $$$n \times m$$$. В начале игры $$$a_{i,j}$$$ кубиков поставлены друг на друга в клетке $$$(i,j)$$$. Две клетки называются соседними, если у них есть общая сторона. Игрок может делать следующие ходы:
- поставить по одному кубику на две соседние клетки;
- поставить два кубика в одну клетку.
Упомянутые кубики все одинаковой высоты.
Пример игры изображен на картинке. Состояния справа достигаются с помощью выполнения данных ходов из состояния слева, и после хода добавляются серые кубики.
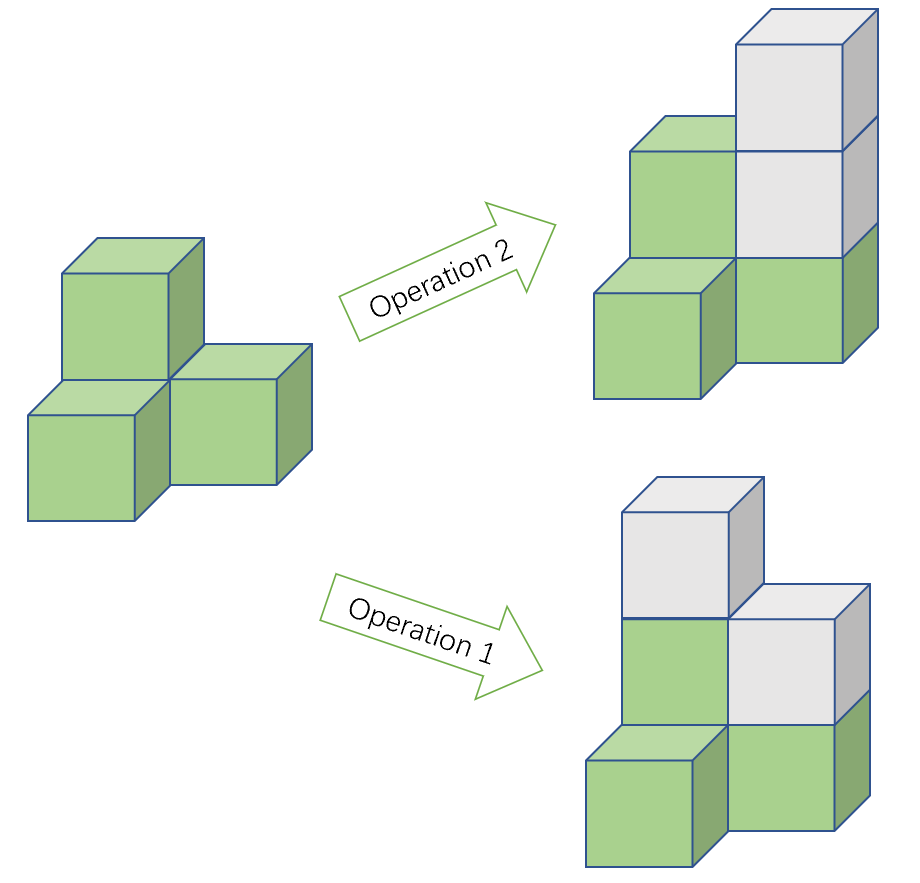
Цель игрока — сделать высоты всех клеток одинаковыми (то есть в каждой клетке должно быть одинаковое количество кубиков) при помощи данных ходов.
Алиса обнаружила, что на некоторых начальных полях невозможно достичь цели, какие бы ходы игрок не делал. Поэтому ей стало интересно, сколько существует таких начальных полей, что
- $$$L \le a_{i,j} \le R$$$ для всех $$$1 \le i \le n$$$, $$$1 \le j \le m$$$;
- игрок может достичь цели, используя данные ходы.
Пожалуйста, помогите Алисе с этим. Обратите внимание, что ответ может быть довольно большой, поэтому выведите его по модулю $$$998,244,353$$$.
В единственной строке записаны четыре целых числа $$$n$$$, $$$m$$$, $$$L$$$ и $$$R$$$ ($$$1\le n,m,L,R \le 10^9$$$, $$$L \le R$$$, $$$n \cdot m \ge 2$$$).
Выведите одно целое число, обозначающее ответ по модулю $$$998,244,353$$$.
2 2 1 1
1
1 2 1 2
2
В первом примере единственное поле, которое удовлетворяет условиям — это $$$a_{1,1}=a_{2,1}=a_{1,2}=a_{2,2}=1$$$. Поэтому ответ $$$1$$$.
Во втором примере начальные поля, которые удовлетворяют условиям, — это $$$a_{1,1}=a_{1,2}=1$$$ и $$$a_{1,1}=a_{1,2}=2$$$. Поэтому ответ $$$2$$$.
| Название |
|---|




