У короля Берляндии Поликарпа LXXXIV есть $$$n$$$ дочерей. Чтобы показать свою власть соседним королевствам, он хочет выдать своих дочерей замуж за принцев этих королевств. По счастливой случайности других королевств так же $$$n$$$.
Поликарп LXXXIV занумеровал своих дочерей от $$$1$$$ до $$$n$$$ и королевства от $$$1$$$ до $$$n$$$. Дальше для каждой дочери он собрал списки королевств, за принцев которых она хочет выйти замуж.
Поликарп LXXXIV — очень занятой правитель, поэтому он просто жадно находит пару своим дочерям одну за другой.
Для первой дочери он выбирает королевство с наименьшим номером из ее списка и выдает дочь за их принца. Для второй дочери он выбирает королевство с наименьшим номером из ее списка, принц которой еще не женат. Если нет неженатых принцев в списке, то дочь не выходит замуж ни за кого, а Поликарп LXXXIV переходит к следующей дочери. Процесс заканчивается после $$$n$$$-й дочери.
Например, пусть будет $$$4$$$ дочери и королевства, списки дочерей: $$$[2, 3]$$$, $$$[1, 2]$$$, $$$[3, 4]$$$, $$$[3]$$$, соответственно.
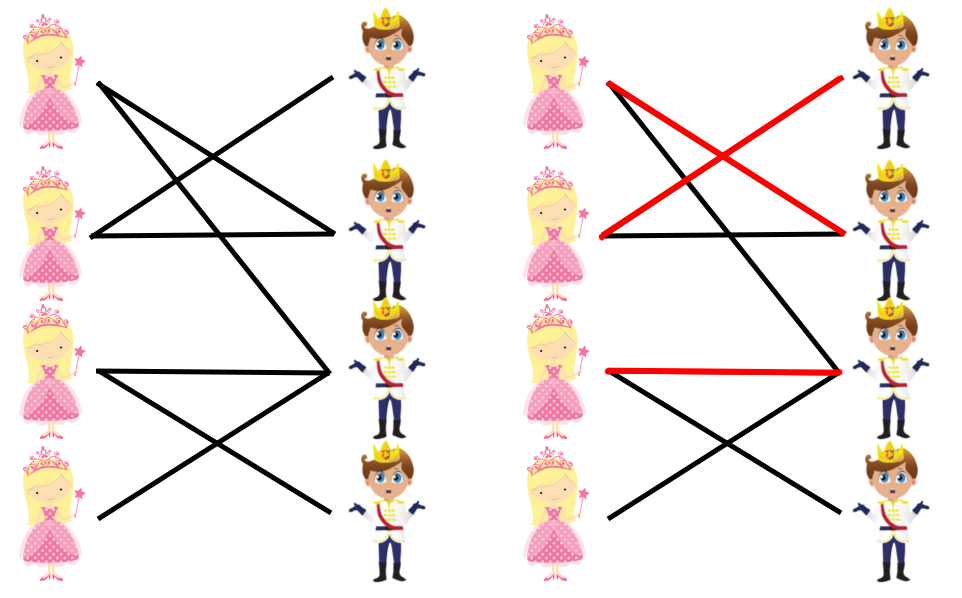
В данном случае дочь $$$1$$$ выходит замуж за принца королевства $$$2$$$, дочь $$$2$$$ выходит замуж за принца королевства $$$1$$$, дочь $$$3$$$ выходит замуж за принца королевства $$$3$$$, оставляя дочь $$$4$$$ без возможности выйти замуж за кого-либо.
На самом деле, до начала всех женитьб у Поликарпа LXXXIV есть время убедить одну из своих дочерей, что за принца какого-либо королевства тоже можно выйти замуж. Фактически, это значит, что он может добавить ровно одно королевство в список ровно одной из своих дочерей. Обратите внимание, что данное королевство не должно содержаться в списке данной дочери.
Поликарп LXXXIV хочет увеличить количество женатых пар.
К сожалению, на что у него нет времени, так это на нахождение записи, которую стоит добавить. Если не существует способа увеличить количество женатых пар, то сообщите, что женитьбы уже оптимальны. Иначе найдите такую запись, после добавления которой итоговое количество женатых пар увеличится.
Если существует несколько способов добавить одну запись так, что количество женатых пар увеличится, то выведите любой из них.
Для вашего и нашего удобства мы просим вас ответить на $$$t$$$ независимых наборов тестовых данных.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов тестовых данных.
Затем следуют $$$t$$$ наборов тестовых данных.
В первой строке каждого набора записано одно целое число $$$n$$$ ($$$1 \le n \le 10^5$$$) — количество дочерей и количество королевств.
В каждой из следующих $$$n$$$ строк дано описание списка каждой дочери. Первое целое число $$$k$$$ ($$$0 \le k \le n$$$) — это количество записей в списке $$$i$$$-й дочери. Затем следуют $$$k$$$ различных чисел $$$g_i[1], g_i[2], \dots, g_i[k]$$$ ($$$1 \le g_i[j] \le n$$$) — номера королевств в списке в возрастающем порядке ($$$g_i[1] < g_i[2] < \dots < g_i[k]$$$).
Гарантируется, что суммарное количество дочерей по всем наборам тестовых данных не превосходит $$$10^5$$$.
Также гарантируется, что суммарное количество королевств в списках по всем наборам тестовых данных не превосходит $$$10^5$$$.
Выведите ответ на каждый тест.
Выведите «IMPROVE» в первой строке, если Поликарп LXXXIV может добавить одно королевство в список одной из его дочерей так, чтобы итоговое количество женатых пар увеличилось. Во второй строке выведите два целых числа — номер дочери и номер королевства, которое Поликарп LXXXIV должен добавить в список данной дочери.
Если существует несколько способов добавить одну запись так, что количество женатых пар увеличится, то выведите любой из них.
В противном случае выведите одно слово «OPTIMAL».
5 4 2 2 3 2 1 2 2 3 4 1 3 2 0 0 3 3 1 2 3 3 1 2 3 3 1 2 3 1 1 1 4 1 1 1 2 1 3 1 4
IMPROVE 4 4 IMPROVE 1 1 OPTIMAL OPTIMAL OPTIMAL
Первый набор входных данных изображен на картинке в условии. Добавление четвертого королевства в список четвертой дочери позволит ей выйти замуж за принца четвертого королевства.
Во втором наборе входных данных любая новая запись увеличит количество женатых пар с $$$0$$$ до $$$1$$$.
В третьем и четвертом наборах входных данных не существует способа добавить запись.
В пятом наборе входных данных не существует способа изменить количество женитьб добавлением новой записи.
| Название |
|---|




