| Codeforces Round 628 (Div. 2) |
|---|
| Закончено |
Идет 5555-й год. У вас есть граф, и вы хотите найти длинный цикл и огромный независимый набор просто потому, что можете. Но пока что вы хотите найти хоть одно из двух.
Для связного графа с $$$n$$$ вершинами вы можете или:
- найти независимое множество с ровно $$$\lceil\sqrt{n}\rceil$$$ вершинами.
- найти простой цикл длиной не менее $$$\lceil\sqrt{n}\rceil$$$.
Независимое множество — это множество вершин такое, что никакие две вершины из него не связаны ребром. Простой цикл — это цикл, который не содержит ни одной вершины дважды. Гарантировано, что вы всегда можете решить хотя бы одну из этих задач.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$5 \le n \le 10^5$$$, $$$n-1 \le m \le 2 \cdot 10^5$$$) — количество вершин и ребер в графе.
Каждая из следующих $$$m$$$ строк содержит два разделенных пробелом целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), которые означают, что между вершинами $$$u$$$ и $$$v$$$ есть ребро. Гарантируется, что граф связен и не содержит никаких петель или двойных ребер.
Если вы решили решить первую задачу, то в первой строке выведите 1, а затем строку, содержащую $$$\lceil\sqrt{n}\rceil$$$ различных целых чисел, не превышающих $$$n$$$, вершины в желаемом независимом наборе.
Если вы решили решить вторую задачу, то в первой строке выведите 2, затем строку, содержащую одно целое число $$$c$$$, представляющее длину найденного цикла, за которой следует строка, содержащая $$$c$$$ различных целых чисел, не превышающих $$$n$$$ — вершины в нужном цикле, в порядке, в котором они идут в цикле.
6 6 1 3 3 4 4 2 2 6 5 6 5 1
1 1 6 4
6 8 1 3 3 4 4 2 2 6 5 6 5 1 1 4 2 5
2 4 1 5 2 4
5 4 1 2 1 3 2 4 2 5
1 3 4 5
В первом примере:
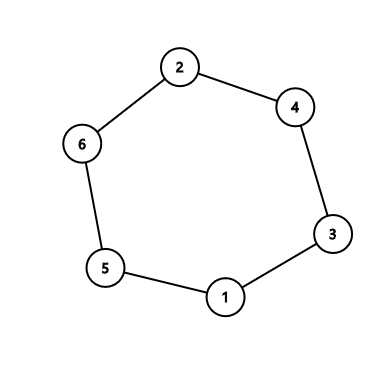
Обратите внимание, что вы можете решить обе задачи, поэтому вывод цикла $$$2-4-3-1-5-6$$$ также является решением.
Во втором примере:
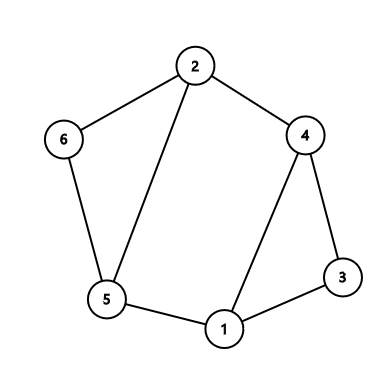
Обратите внимание, что если есть несколько ответов, вы можете вывести любой, поэтому, например, вывод цикла $$$2-5-6$$$ разрешен.
В третьем примере:
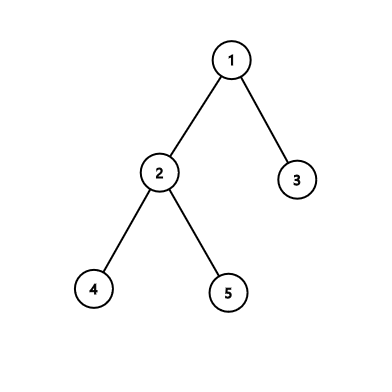
| Название |
|---|




