| Codeforces Round 627 (Div. 3) |
|---|
| Закончено |
Вам задано дерево, состоящее из $$$n$$$ вершин. Деревом называется связный неориентированный граф с $$$n-1$$$ ребром. Каждая вершина $$$v$$$ этого дерева имеет свой цвет ($$$a_v = 1$$$, если вершина $$$v$$$ белая, и $$$0$$$, если вершина $$$v$$$ черная).
Вам нужно решить следующую задачу для каждой вершины $$$v$$$: какую максимальную разницу между количеством белых вершин и количеством черных вершин вы можете получить, если выберете некоторое поддерево заданного дерева, которое содержит вершину $$$v$$$? Поддеревом дерева называется связный подграф заданного дерева. Более формально, если вы выберете поддерево, которое содержит $$$cnt_w$$$ белых вершин и $$$cnt_b$$$ черных вершин, вам нужно максимизировать $$$cnt_w - cnt_b$$$.
Первая строка теста содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Вторая строка теста содержит $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$0 \le a_i \le 1$$$), где $$$a_i$$$ — это цвет $$$i$$$-й вершины.
Каждая из последующих $$$n-1$$$ строк описывает ребро в дереве. Ребро $$$i$$$ задается двумя целыми числами $$$u_i$$$ и $$$v_i$$$ — номерами вершин, которые оно соединяет $$$(1 \le u_i, v_i \le n, u_i \ne v_i$$$).
Гарантируется, что заданные ребра образуют дерево.
Выведите $$$n$$$ целых чисел $$$res_1, res_2, \dots, res_n$$$, где $$$res_i$$$ — максимальная возможная разница между количеством белых и количеством черных вершин в некотором поддереве, которое содержит вершину $$$i$$$.
9 0 1 1 1 0 0 0 0 1 1 2 1 3 3 4 3 5 2 6 4 7 6 8 5 9
2 2 2 2 2 1 1 0 2
4 0 0 1 0 1 2 1 3 1 4
0 -1 1 -1
Первый тестовый пример представлен ниже:
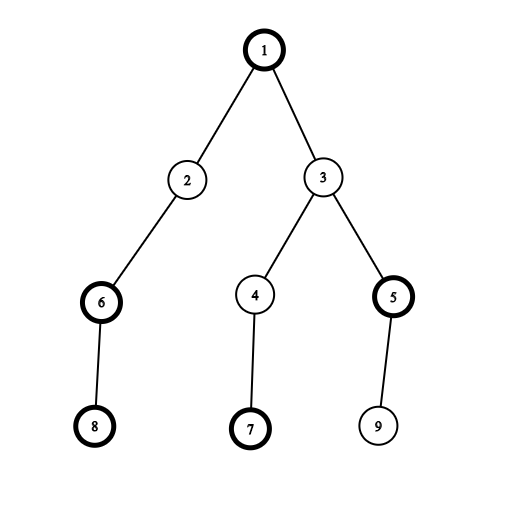
Черные вершины выделены жирным.
Во втором тестовом примере лучшими поддеревьями для вершин $$$2, 3$$$ и $$$4$$$ являются вершины $$$2, 3$$$ и $$$4$$$ соответственно. И лучшим поддеревом для вершины $$$1$$$ является поддерево, состоящее из вершин $$$1$$$ и $$$3$$$.
| Название |
|---|




