| Codeforces Round 627 (Div. 3) |
|---|
| Закончено |
Слева от строки $$$s = s_1 s_2 \ldots s_n$$$, состоящей из $$$n$$$ символов, находится лягушка (точнее, изначально лягушка находится в клетке $$$0$$$). Каждый символ строки $$$s$$$ — это или 'L', или 'R'. Это значит, что если лягушка находится в $$$i$$$-й клетке и $$$i$$$-й символ — это 'L', то она может прыгать только влево. Если лягушка стоит в $$$i$$$-й клетке и $$$i$$$-й символ — это 'R', то она может прыгать только вправо. Из клетки $$$0$$$ лягушка может прыгать только вправо.
Заметим, что лягушка может прыгать в одну и ту же клетку дважды и может совершить столько прыжков, сколько ей потребуется.
Лягушка хочет достичь $$$n+1$$$-й клетки. Лягушка выбирает некоторое целое положительное значение $$$d$$$ перед самым первым прыжком (и потом не может изменить его) и прыгает не более, чем на $$$d$$$ клеток за раз. То есть, если $$$i$$$-й символ — 'L', то лягушка может прыгнуть в любую клетку из отрезка $$$[max(0, i - d); i - 1]$$$, а если $$$i$$$-й символ — 'R', то лягушка может прыгнуть в любую клетку из отрезка $$$[i + 1; min(n + 1; i + d)]$$$.
Лягушка не хочет прыгать слишком далеко, поэтому ваша задача — найти минимальное возможное значение $$$d$$$, при котором лягушка сможет достичь клетки $$$n+1$$$ из клетки $$$0$$$, если будет прыгать не более, чем на $$$d$$$ клеток за раз. Гарантируется, что всегда возможно достичь $$$n+1$$$ из $$$0$$$.
Вам нужно ответить на $$$t$$$ независимых наборов входных данных.
Первая строка теста содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Следующие $$$t$$$ строк описывают наборы входных данных. $$$i$$$-й описан строкой $$$s$$$ состоящей из не менее, чем $$$1$$$, и не более, чем $$$2 \cdot 10^5$$$ символов 'L' и 'R'.
Гарантируется, что сумма длин строк по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$ ($$$\sum |s| \le 2 \cdot 10^5$$$).
Для каждого набора входных данных выведите ответ — минимальное возможное значение $$$d$$$, при котором лягушка может достичь клетки $$$n+1$$$ из клетки $$$0$$$, если будет совершать прыжки длиной не более, чем $$$d$$$.
6 LRLRRLL L LLR RRRR LLLLLL R
3 2 3 1 7 1
Картинка, описывающая первый набор тестовых данных из примера и один из возможных ответов:
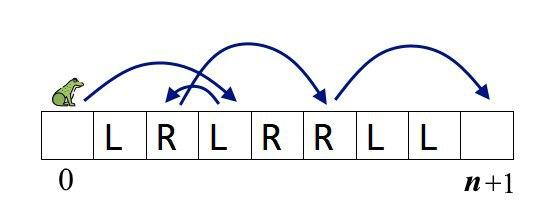
Во втором наборе тестовых данных из примера лягушка может прыгнуть только напрямую из $$$0$$$ в $$$n+1$$$.
В третьем наборе тестовых данных лягушка может выбрать $$$d=3$$$, прыгнуть в клетку $$$3$$$ из клетки $$$0$$$ и затем прыгнуть в клетку $$$4$$$ из клетки $$$3$$$.
В четвертом наборе тестовых данных из примера лягушка может выбрать $$$d=1$$$ и прыгнуть $$$5$$$ раз вправо.
В пятом наборе тестовых данных из примера лягушка может прыгнуть только напрямую из $$$0$$$ в $$$n+1$$$.
В шестом наборе тестовых данных из примера лягушка может выбрать $$$d=1$$$ и прыгнуть $$$2$$$ раза вправо.
| Название |
|---|




